已知等差数列 满足:
满足: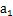 =2,且
=2,且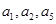 成等比数列.
成等比数列.
(1)求数列 的通项公式.
的通项公式.
(2)记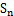 为数列
为数列 的前n项和,是否存在正整数n,使得
的前n项和,是否存在正整数n,使得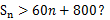 若存在,求n的最小值;若不存在,说明理由.
若存在,求n的最小值;若不存在,说明理由.
在 中,角A,B,C所对的边分别为a,b,c,已知
中,角A,B,C所对的边分别为a,b,c,已知 .
.
(1)当 ,且
,且 的面积为
的面积为 时,求a的值;
时,求a的值;
(2)当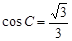 时,求
时,求 的值.
的值.
某中学从高中三个年级选派4名教师和20名学生去当文明交通宣传志愿者,20名学生的名额分配为高一12人,高二6人,高三2人.
(1)若从20名学生中选出3人做为组长,求他们中恰好有1人是高一年级学生的概率;
(2)若将4名教师随机安排到三个年级(假设每名教师加入各年级是等可能的,且各位教师的选择是相互独立的),记安排到高一年级的教师人数为X,求随机变量X的分布列和数学期望.
已知函数
 .
.
(1)求 的最小正周期和最小值;
的最小正周期和最小值;
(2)若 ,
, 且
且 ,求
,求 的值.
的值.
已知函数
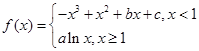 的图像过坐标原点
的图像过坐标原点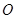 ,且在点
,且在点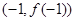 处的切线的斜率是
处的切线的斜率是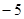 .
.
(1)求实数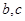 的值;
的值;
(2)求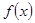 在区间
在区间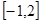 上的最大值;
上的最大值;
(3)对任意给定的正实数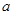 ,曲线
,曲线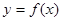 上是否存在两点
上是否存在两点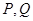 ,使得
,使得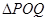 是以
是以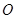 为直角顶点的直角三角形,且此三角形斜边的中点在
为直角顶点的直角三角形,且此三角形斜边的中点在 轴上?请说明理由.
轴上?请说明理由.
已知动圆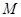 与直线
与直线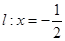 相切且与圆
相切且与圆 :
: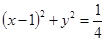 外切。
外切。
(1)求圆心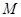 的轨迹
的轨迹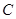 方程;
方程;
(2)过定点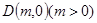 作直线
作直线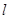 交轨迹
交轨迹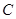 于
于 两点,
两点,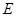 是
是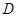 点关于坐标原点
点关于坐标原点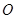 的对称点,求证:
的对称点,求证: ;
;