小物块A的质量为m,物块与坡道间的动摩擦因数为μ,水平面光滑,坡道顶端距水平面高度为h,倾角为θ,物块从坡道进入水平滑道时,在底端O点处无机械能损失,重力加速度为g. 将轻弹簧的一端连接在水平滑道M处并固定在墙上,另一自由端恰位于坡道的底端O点,如图所示.物块A从坡顶由静止滑下,求:
(1)物块滑到O点时的速度大小;
(2)弹簧为最大压缩量d时的弹性势能;
(3)物块A被弹回到坡道上升的最大高度。
我国南宋远洋商贸船“南海一号”于2007年成功打捞出水.为复原我国海上丝绸之路历史提供了极其珍贵的实物资料,采用沉井包裹沉船的整体打捞方式,在世界水下考古也是一大创新。某同学为了体验“南海一号”的打捞过程,特利用滑轮组从水下打捞一重物。
如图所示,用一个底面积S=0.05m2、高h=0.2m的长方体形状的重物模拟“南海一号”,该同学站在岸边拉动绳子自由端,使重物从水底开始向上运动,假定重物一直做竖直向上的匀速直线运动,并经历三个运动阶段:第一阶段,从重物在水度开始运动到重物的上表面面刚露出水面,绳对重物的拉力 F1="140" N, 用时t1=40s,第二阶段,从重物上表面刚露出水面到其下表面刚离开水面,用时t2=4s,第三阶段,从重物下表面离开水面后在空中上升, 已知动滑轮所受重力G0="60" N, ρ水=1.0×103kg/m3, g=10N/g,不计绳重、轮与轴之间的摩擦及水的阻力,不考虑重物出水前后质量的变化。求:
①在第一阶段运动中,水对重物的浮力F浮为多大?
②在第一阶段运动中,绳对重物做功W1为多大?
③滑轮组在第一阶段运动中的机械效率η1和第三阶段运动中的机械效率η3分別为多大?
如图甲所示,在2015年某工厂要研发一种新型材料,要求对该材料的承受的撞击力进行测试。在测试时将材料样品(不计质量)平放在压力传感器上,闭合开关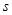 ,由静止自由释放重物,经撞击后样品材料仍完好无损。从重物开始下落到撞击样品的这个过程中,电流表的示数
,由静止自由释放重物,经撞击后样品材料仍完好无损。从重物开始下落到撞击样品的这个过程中,电流表的示数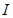 随时间
随时间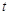 变化的图像如图乙所示,压力传感器的电阻R随压力
变化的图像如图乙所示,压力传感器的电阻R随压力 变化的图像如图丙所示。电源的电压=24V,定值电阻R0=10Ω。求:
变化的图像如图丙所示。电源的电压=24V,定值电阻R0=10Ω。求:
(1)在重物下落的过程中, 压力传感器的电阻是多少?
(2)在撞击过程中,样品受到的最大撞击力是多少?
如图甲所示,电源电压恒定,R0为定值电阻。将滑动变阻器的滑片从a端滑到b端的过程中,电压表示数U与电流表示数I间的关系图象如图乙所示。求: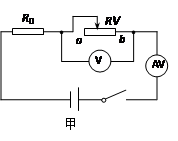

(1)滑动变阻器R的最大阻值;
(2)R0的阻值及电源电压;
(3)当滑片滑到滑动变阻器的中点时,电阻R0消耗的功率。
小明是个很善于把物理知识应用于实际的同学,最近他家中新安装了天然气热水器,如图所示。小明仔细观察了包装箱、热水器铭牌,获得了以下信息:①包装箱及热水器的总质量为16kg;②“堆码层数极限”标志数为11,即该包装箱在仓储时从地面开始,平放时最大堆放层数是11层,超过则可能把最底层的包装箱压坏;③根据包装箱尺寸计算出平放时的底面积为0.4m2 ;④热效率为87%。表示该热水器工作时,天然气完全燃烧所消耗的化学能,有87%的转化为水的内能;⑤加热模式为“即热式”。即用热水器给水加热时,只要接通开关让自来水流过热水器,流出的水即可达到设定的水温。
水暖想估测该热水器的实际热效率,以核对铭牌上的数值是否准确。他接通热水器工作开关,当流出40kg热水时,让热水器停止工作。已知当时自来水的温度是15℃,热水器输出的热水温度为40℃,观察天然气表得知共用了0.15m3的天然气,天然气的热值为3.2×107J/m3,水的比热容4.2×103J/(kg·℃),g取10N/kg。
请帮小明解答下列问题:

(1)若在仓储时堆码层达到了极限11层,则最下层的包装箱承受的压强是多大?
(2)小明在估测过程中,①流过热水器的水吸收的热量是多少?②天然气完全燃烧释放的热量是多少?
(3)该热水器的实际效率是多少?
如图甲是用来焊接自来水管的塑料热熔器,通电后,加热头发热,使需对接的塑料水管的两头熔化,将它们对接,紧压在一起,冷却后就可以焊接成一根水管了,其电路部分如图乙所示,S1是手控开关,S2为温控开关,ND为指示灯,R1是限流电阻,R2和R3为电热丝,表是它的术参数.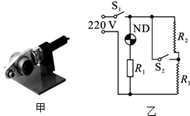
| 产品名称 |
便携式自动控温式PPR/PP•R塑料管材 |
| 型号 |
20-32MM(配Φ20、Φ25、Φ32模头) |
| 环境温度 |
-20℃-50℃ |
| 额定电压 |
220V |
| 加头温度 |
260±5℃ |
| 功率 |
加热状态电热丝功率:1000W 保温状态电丝功率:250W |
| 安全指标 |
绝缘电阻不小于1MΩ |
请解答下列问题:
(1)若指示灯ND用“3V 10mA”的发光二极管,则限流电阻R1的阻值多大才能使指示灯正常发光?
(2)电热丝R2的阻值多大?
(3)当环境温度是20℃时,熔化1kg的PVC塑料需要吸收106J热量,此时塑料热熔器的效率为90%.某次熔接需要熔化90g的PVC,在塑料热熔器正常工作情况下需要加热多长时间?