在2014年巴西世界杯足球赛开幕之前,某校团支部为了解本校学生对世界杯足球赛的关注情况,随机调查了部分学生对足球运动的喜欢程度,绘制成如下的两幅不完整的统计图.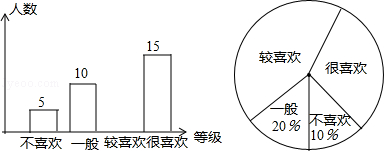
请你根据以上统计图提供的信息,回答下列问题:
(1)随机抽查了 名学生;
(2)补全图中的条形图;
(3)若全校共有500名学生,请你估计全校大约有多少名学生喜欢(含“较喜欢”和“很喜欢”)足球运动.
应用无刻度的直尺画图: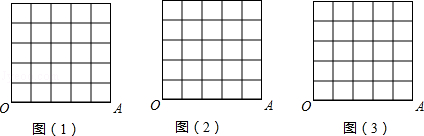
在下面的三个图中,以OA为边,在正方形网格内作∠AOB=α,B点为格点(每个小正方形的顶点)使sinα的值分别为: ,
,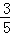 和
和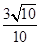 .
.
解不等式组并把解集在数轴上表示出来: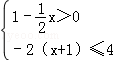 .
.
如图,抛物线y=(x+m)2+m,与直线y=﹣x相交于E,C两点(点E在点C的左边),抛物线与x轴交于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=﹣x相交于点D.
(1)若抛物线与y轴的交点坐标为(0,2),求m的值;
(2)求证:⊙H与直线y=1相切;
(3)若DE=2EC,求⊙H的半径.
如图,△ABC为等边三角形.O为BC的中垂线AH上的动点,⊙O经过B,C两点,D为弧上一点,D,A两点在BC边异侧,连接AD,BD,CD.
(1)如图1,若⊙O经过点A,求证:BD+CD=AD;
(2)如图2,圆心O在BD上,若∠BAD=45°;求∠ADB的度数;
(3)如图3,若AH=OH,求证:BD2+CD2=AD2.
某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(100﹣x)件.设这段时间内售出该商品的利润为y元.
(1)直接写出利润y与售价x之间的函数关系式;
(2)当售价为多少元时,利润可达1000元;
(3)应如何定价才能使利润最大?