如图，已知直线AB经过⊙O上的点C，且OA=OB，CA=CB．
（1）求证：直线AB是⊙O的切线．
（2）若∠A=34°，AC=6，求⊙O的周长．（结果精确到0.01）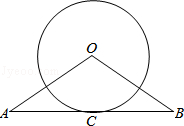
如图，直线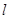
：
分别与
轴、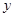
轴交于A、B两点，点C线段AB上，作CD⊥x轴于D, CD="2OD," 点E线段OB上,且AE=BE；
（1）填空：点C的坐标为（ ， ）；点E的坐标为（ ， ）；
（2）直线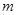
过点E，且将△AOB分成面积比为1：2的两部分，求直线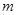的表达式；
（3）点P在x轴上运动，
①当PC+PE取最小值时，求点P的坐标及PC+PE的最小值；
②当PC-PE取最大值时，求点P的坐标及PC-PE的最大值；
如图，直线AB与x轴负半轴、y轴正半轴分别交于A、B两点，OA、OB的长度分别为a和b，且满足
，直线OQ与直线AB交于点Q，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM=9，BN=4，求MN的长．
如图，直线y =" 2x" + 3与x轴相交于点A，与y轴相交于点B．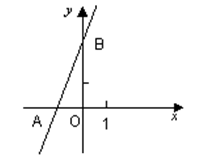
（1）求A，B两点的坐标；
（2）过B点作直线BP与x轴的正半轴相交于P，且使OP = 2OA，求ΔABP的面积．
某弹簧的自然长度为3cm,在弹簧限度内,所挂物体的质量x每增加1kg,弹簧长度y增加0．5cm．
（1）计算所挂物体的质量分别为1kg、2kg、3kg、4kg、5kg时的弹簧长度,并填入下表:
| x/kg |
0 |
1 |
2 |
3 |
4 |
5 |
| y/cm |
（2）你能写出x与y之间的关系式吗?
一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,他手中持有的钱数（含备用零钱）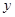
与售出的土豆千克数
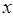的关系如图所示,结合图象回答下列问题．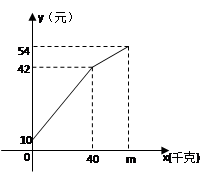
（1）农民自带的零钱是 元；
（2）求降价前y与x之间的函数关系式；
（3）由表达式可求降价前土豆的价格是 元∕千克；
（4）降价后他按每千克0．6元将剩余土豆售完,这时他手中的钱（含备用零钱）是54元,求他一共带的土豆千克数m。