如图,在等腰直角△ABC中,∠ABC=90°,AB=BC=4,P为AC中点,E为AB边上一动点,F为BC边上一动点,且满足条件∠EPF=45°,记四边形PEBF的面积为S1;
(1)求证:∠APE=∠CFP;
(2)记△CPF的面积为S2,CF=x,y= .
.
①求y关于x的函数解析式和自变量的取值范围,并求y的最大值.
②在图中作四边形PEBF关于AC的对称图形,若它们关于点P中心对称,求y的值.
在一平面内,线段 ,线段 ,将这四条线段顺次首尾相接.把 固定,让 绕点 从 开始逆时针旋转角 到某一位置时, , 将会跟随出现到相应的位置.
论证:如图1,当 时,设 与 交于点 ,求证: ;
发现:当旋转角 时, 的度数可能是多少?
尝试:取线段 的中点 ,当点 与点 距离最大时,求点 到 的距离;
拓展:①如图2,设点 与 的距离为 ,若 的平分线所在直线交 于点 ,直接写出 的长(用含 的式子表示);
②当点 在 下方,且 与 垂直时,直接写出 的余弦值.
如图是某同学正在设计的一动画示意图, 轴上依次有 , , 三个点,且 ,在 上方有五个台阶 (各拐角均为 ,每个台阶的高、宽分别是1和1.5,台阶 到 轴距离 .从点 处向右上方沿抛物线 发出一个带光的点 .
(1)求点 的横坐标,且在图中补画出 轴,并直接指出点 会落在哪个台阶上;
(2)当点 落到台阶上后立即弹起,又形成了另一条与 形状相同的抛物线 ,且最大高度为11,求 的解析式,并说明其对称轴是否与台阶 有交点;
(3)在 轴上从左到右有两点 , ,且 ,从点 向上作 轴,且 .在 沿 轴左右平移时,必须保证(2)中沿抛物线 下落的点 能落在边 (包括端点)上,则点 横坐标的最大值比最小值大多少?
注:(2)中不必写 的取值范围

如图, 的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为 为 的整数),过点 作 的切线交 延长线于点 .
(1)通过计算比较直径和劣弧 长度哪个更长;
(2)连接 ,则 和 有什么特殊位置关系?请简要说明理由;
(3)求切线长 的值.
如图是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点 始终以 的速度在离地面 高的上空匀速向右飞行,2号试飞机(看成点 一直保持在1号机 的正下方.2号机从原点 处沿 仰角爬升,到 高的 处便立刻转为水平飞行,再过 到达 处开始沿直线 降落,要求 后到达 处.
(1)求 的 关于 的函数解析式,并直接写出2号机的爬升速度;
(2)求 的 关于 的函数解析式,并预计2号机着陆点的坐标;
(3)通过计算说明两机距离 不超过 的时长是多少.
注:(1)及(2)中不必写 的取值范围

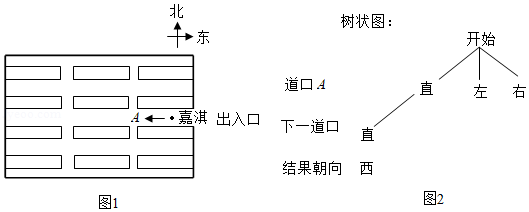
某博物馆展厅的俯视示意图如图1所示.嘉淇进入展厅后开始自由参观,每走到一个十字道口,她自己可能直行,也可能向左转或向右转,且这三种可能性均相同.
(1)求嘉淇走到十字道口 向北走的概率;
(2)补全图2的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.