已知:在平面直角坐标系中,点A、B分别在x轴正半轴上,且线段OA、OB(OA<OB)的长分别等于方程x2﹣5x+4=0的两个根,点C在y轴正半轴上,且OB=2OC.
(1)试确定直线BC的解析式;
(2)求出△ABC的面积.
为了了解本校2014-2015学年七年级学生的身体素质情况,体育老师随机抽取了本校50名2014-2015学年七年级学生进行一分钟跳绳次数测试,测试所得样本数据(单位:次)如下:
88 90 92 96 99 102 106 108 110 112
113 115 115 117 118 120 120 123 125 127
130 132 134 134 134 135 136 137 138 138
139 141 142 142 143 144 145 146 148 149
150 152 153 157 160 162 162 165 168 172
(1)记跳绳次数为x,补全下面的样本频数分布表与频数分布直方图:
| 组别 |
次数(x) |
频数(人数) |
| 1 |
80≤x<100 |
5 |
| 2 |
100≤x<120 |
|
| 3 |
120≤x<140 |
|
| 4 |
140≤x<160 |
|
| 5 |
160≤x<180 |
(2)若该年级有300名学生,请根据样本数据估计该校2014-2015学年七年级学生中一分钟跳绳次数不低于120次的学生大约有多少人?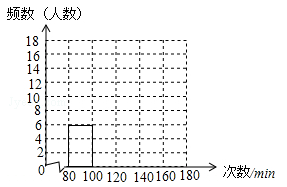
解不等式组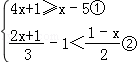 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
解方程组:
(1)
(2) .
.
欧拉是一位著名的数学家,他把他的一生都献给了人类的数学事业,在他一生岁数的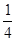 那年,他发表了第一篇数学论文,并且获得了巴黎科学院奖金,此后过了7年,他成为彼得堡科学院的数学教授,在欧拉去世的前17年,他不幸双目失明了,但他继续在黑暗的世界里凭着他的记忆和心算进行数学研究,在这17年里,他写出了数学论文400篇,正好是他一生的岁数与他成为彼得堡学院数学教授时岁数之差的8倍.根据以上信息,请你算出数学家欧拉一生活了多少岁?
那年,他发表了第一篇数学论文,并且获得了巴黎科学院奖金,此后过了7年,他成为彼得堡科学院的数学教授,在欧拉去世的前17年,他不幸双目失明了,但他继续在黑暗的世界里凭着他的记忆和心算进行数学研究,在这17年里,他写出了数学论文400篇,正好是他一生的岁数与他成为彼得堡学院数学教授时岁数之差的8倍.根据以上信息,请你算出数学家欧拉一生活了多少岁?
如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.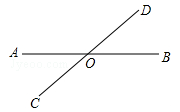
(1)求∠BOD的度数;
(2)以O为端点引射线OE、OF,射线OE平分∠BOD,且∠EOF=90°,求∠BOF的度数,并画图加以说明.