“校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对学生带手机现象的看法,统计整理并制作了如下的统计图:
(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的家长大约有多少名?
补全证明过程
已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。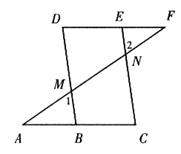
证明:∵∠1=∠2(已知),
又∠1=∠DMN(___________________),
∴∠2=∠_________(等量代换)。
∴DB∥EC(同位角相等,两直线平行)。
∴∠A=∠F(两直线平行,内错角相等)。
已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
| △ABC |
A(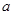 ,0) ,0) |
B(3,0) |
C(5,5) |
| △A′B′C′ |
A′(4,2) |
B′(7,b) |
C′(c,7) |
(1)观察表中各对应点坐标的变化,并填空: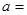 __________,
__________,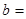 __________,
__________,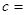 __________;
__________;
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′
(3)直接写出△A′B′C′的面积是__________。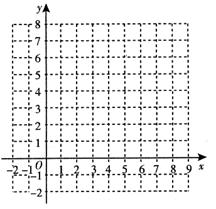
已知:关于x,y的方程组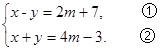 的解为负数,求m的取值范围.
的解为负数,求m的取值范围.
(1)解不等式3(x+1)<4(x-2)-3,并把它的解集表示在数轴上;
(2).求不等式组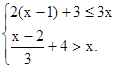 的整数解.
的整数解.
如图,抛物线 与
与 轴的交点为A、B,与
轴的交点为A、B,与 轴的交点为C,顶点为
轴的交点为C,顶点为 ,将抛物线
,将抛物线 绕点B旋转
绕点B旋转 ,得到新的抛物线
,得到新的抛物线 ,它的顶点为D.
,它的顶点为D.
(1)求抛物线 的解析式;
的解析式;
(2)设抛物线 与
与 轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为
轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为 ,△PEF的面积为S,求S与
,△PEF的面积为S,求S与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围;
的取值范围;
(3)设抛物线 的对称轴与
的对称轴与 轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.