某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ)从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
选修4-5:不等式选讲
设函数 ,
, .
.
(1)求不等式 的解集;
的解集;
(2)设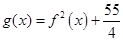 ,且
,且 .求证:
.求证: .
.
(本小题满分10分)选修4-4:坐标系与参数方程
已知椭圆C: ,直线
,直线 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的参数方程及直线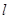 的普通方程;
的普通方程;
(Ⅱ)设 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线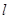 的距离相等,求点P的坐标.
的距离相等,求点P的坐标.
如图, 是△
是△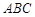 的外接圆,D是
的外接圆,D是 的中点,BD交AC于E.
的中点,BD交AC于E.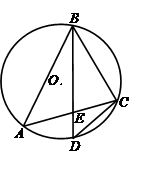
(Ⅰ)求证: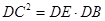 ;
;
(Ⅱ)若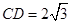 ,O到AC的距离为1,求⊙O的半径
,O到AC的距离为1,求⊙O的半径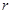
(本小题满分12分)已知函数 .
.
(Ⅰ)当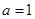 时,证明:当
时,证明:当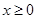 时,
时,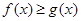 ;
;
(Ⅱ)当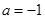 时,证明:
时,证明: .
.
(本小题满分12分)在平面直角坐标系 中,已知椭圆
中,已知椭圆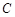 :
: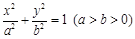 的离心率
的离心率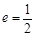 ,直线
,直线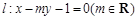 过椭圆
过椭圆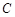 的右焦点
的右焦点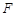 ,且交椭圆
,且交椭圆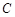 于
于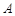 ,
,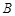 两点.
两点.
(1)求椭圆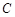 的标准方程;
的标准方程;
(2)已知点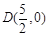 ,连结
,连结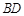 ,过点
,过点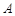 作垂直于
作垂直于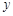 轴的直线
轴的直线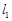 ,设直线
,设直线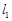 与直线
与直线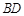 交于点
交于点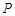 ,试探索当
,试探索当 变化时,是否存在一条定直线
变化时,是否存在一条定直线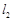 ,使得点
,使得点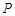 恒在直线
恒在直线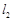 上?若存在,请求出直线
上?若存在,请求出直线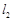 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.