(本题共2小题,每小题5分,共10分)
(Ⅰ)已知函数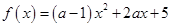 为偶函数,求实数
为偶函数,求实数 的值;
的值;
(Ⅱ)已知角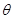 的终边经过点
的终边经过点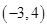 ,求
,求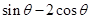 的值.
的值.
(本小题满分12)已知中心在坐标原点O的椭圆C经过点A(2,3),且
点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线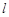 ,使得直线
,使得直线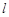 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与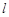 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线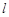 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
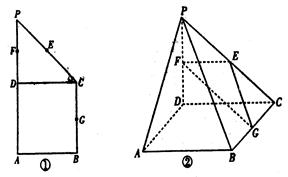
(本小题满分12)如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使PD⊥平面ABCD(如图②)
(1)求证AP∥平面EFG;
(2)求平面EFG与平面PDC所成角的大小;
(3)求点A到平面EFG的距离。

(本小题满分10)某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)
(3)把90分以上(包括90分)视为成绩优秀,那么从成绩是60分以上(包括60分)的学生中选一人,求此人成绩优秀的概率。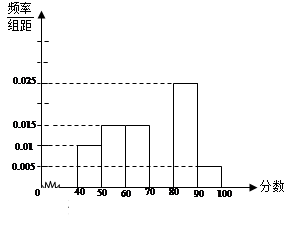
|
(本小题满分10)设命题 ,命题
,命题
 ;如果“
;如果“ ”为真,“
”为真,“ ”为假,求
”为假,求 的取值范围。
的取值范围。