科学研究发现,空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系,经测量,在海拔高度为0米的地方,空气含氧量约为299克/立方米,在海拔高度为2000米的地方,空气含氧量约为235克/立方米.
(1)求出y与x的函数表达式;
(2)已知某山的海拔高度为1400米,请你求出该山山顶处的空气含氧量约为多少?
如图,分别延长□ABCD的边BA、DC到点E、H,使得AE=CH,连接EH,分别交AD、BC于点F、G.求证:△BEG≌△DHF.
已知如图,对称轴为直线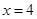 的抛物线
的抛物线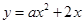 与
与 轴相交于点B、O.
轴相交于点B、O.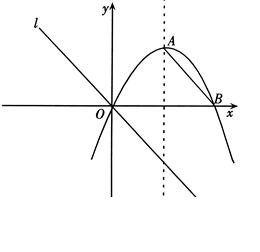
(1)求抛物线的解析式,并求出顶点A的坐标.
(2) 连结AB,平移AB所在的直线,使其经过原点O,得到直线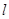 .点
.点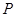 是
是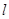 上一动点,当△
上一动点,当△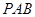 的周长最小时,求点P的坐标.
的周长最小时,求点P的坐标.
(3)当△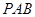 的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似,若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O)
的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似,若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O)
函数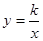 和
和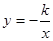
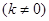 的图象关于
的图象关于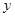 轴对称,我们把函数
轴对称,我们把函数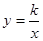 和
和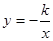
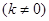 叫做互为“镜子”函数.类似地,如果函数
叫做互为“镜子”函数.类似地,如果函数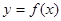 和
和 的图象关于
的图象关于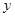 轴对称,那么我们就把函数
轴对称,那么我们就把函数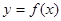 和
和 叫做互为“镜子”函数.
叫做互为“镜子”函数.
(1)请写出函数y=2x-3的“镜子”函数: ▲;
(2)函数 ▲的“镜子”函数是y=-x2+2x+3;
(3)如图,一条直线与一对“镜子”函数 (
(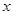 >
> )和
)和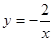 (
(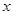 <
< )的图象分别交于点A,B,C,如果
)的图象分别交于点A,B,C,如果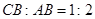 ,点
,点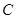 在函数
在函数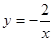 (
(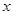 <
< )的“镜子”函数上的对应点的横坐标是1/2,求点
)的“镜子”函数上的对应点的横坐标是1/2,求点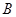 的坐标.
的坐标.
2012年4月11日,印尼北苏门答腊西岸发生里氏8.6级特大地震,造成重大人员伤亡和财产损失.强震发生后,中国军队将筹措到位的第一批援印尼救灾物资打包成件,其中棉帐篷和毛巾被共3200件,毛巾被比棉帐篷多800件.
(1)求打包成件的棉帐篷和毛巾被各多少件?
(2)现计划用甲、乙两种小飞机共8架,一次性将这批棉帐篷和毛巾被全部运往印尼重灾区.已知甲种飞机最多可装毛巾被400件和棉帐篷100件,乙种飞机最多可装毛巾被和棉帐篷各200件.则安排甲、乙两种飞机时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种飞机每架需运输成本费4000元,乙种飞机每架需付运输成本费3600元.应选择哪种方案可使运输成本费最少?最少运输成本费是多少元?
已知:如图,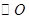 半径
半径 垂直于弦
垂直于弦 ,点
,点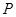 在
在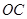 的延长线上,
的延长线上, 平分
平分 .
.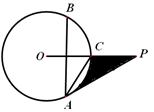
(1) 求证: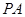 是
是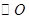 的切线
的切线
(2) 如果 =
=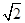 ,
,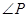 =30°,求阴影部分面积.(保留根号和
=30°,求阴影部分面积.(保留根号和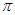 )
)