（1）已知抛物线的顶点在原点，准线方程为
，求抛物线的标准方程；
（2）已知双曲线的焦点在x轴上，且过点（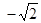
，-
），（
，
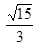），求双曲线的标准方程。
设甲、乙两射手独立地射击同一目标，他们击中目标的概率分别为0．95，0．9．
求：
（1）在一次射击中，目标被击中的概率；
（2）目标恰好被甲击中的概率．
已知随机变量ε的分布列如下表：
| ε |
0 |
1 |
2 |
3 |
4 |
| p |
0．2 |
0．4 |
0．3 |
0．08 |
0．02 |
求其数学期望、方差和标准差．
某一中学生心理咨询中心服务电话接通率为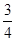
，某班3名同学商定明天分别就同一问题询问该服务中心，且每人只拨打一次，求他们中成功咨询的人数为X的分布列．
在一次口试中，要从10道题中随机抽出3道题进行回答，答对了其中2道题就获得及格，某考生会回答10道题中的6道题，那么他（她）获得及格的概率是多少？
，
, 且
.
的解析式;
时, 
的值.