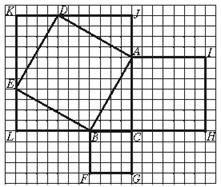
梯形ABCE中,AD∥BC,DC⊥BC,CE⊥AB于点E,点F在边CD上,且BE•CE=BC•CF.
(1)求证:AE•CF=BE•DF;
(2)若点E为AB中点,求证:AD•BC=2EC2-BC2.
如图:要修建一个育苗棚,棚高h="1.8" m,棚宽a="2.4" m,棚的长为12 m,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?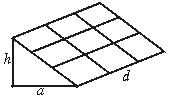
在△ABC中,∠C="90°,AC=2.1" cm,BC="2.8" cm
(1)求这个三角形的斜边AB的长和斜边上的高CD的长;
(2)求斜边被分成的两部分AD和BD的长.
已知一个等腰三角形的底边和腰的长分别为12 cm和10 cm,求这个三角形的面积.
下图甲是任意一个直角三角形ABC,它的两条直角边的边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.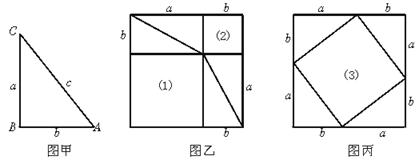
①图乙和图丙中(1)(2)(3)是否为正方形?为什么?
②图中(1)(2)(3)的面积分别是多少?
③图中(1)(2)的面积之和是多少?
④图中(1)(2)的面积之和与正方形(3)的面积有什么关系?为什么?
由此你能得到关于直角三角形三边长的关系吗?
请你观察下列图形,直角三角形ABC的两条直角边的长分别为AC=7,BC=4,请你研究这个直角三角形的斜边AB的长的平方是否等于42+72?