某企业为了改善污水处理条件,决定购买A、B两种型号的污水处理设备共8台,其中每台的价格、月处理污水量如下表:
| |
A型 |
B型 |
| 价 格(万元/台) |
8 |
6 |
| 月处理污水量(吨/月) |
200 |
180 |
经预算,企业最多支出57万元购买污水处理设备,且要求设备月处理污水量不低于1490吨.
(1)企业有哪几种购买方案?
(2)哪种购买方案更省钱?
如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP=°;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.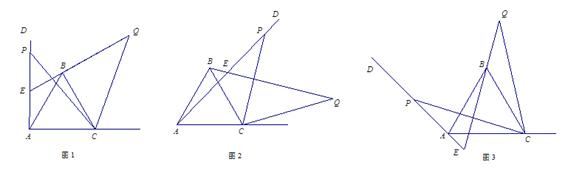
已知:关于x的一元二次方程mx2﹣(4m+1)x+3m+3="0" (m>1).
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2(其中x1>x2),若y是关于m的函数,且y=x1﹣3x2,求这个函数的解析式;
(3)将(2)中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当关于m的函数y=2m+b的图象与此图象有两个公共点时,b的取值范围.
阅读下面材料:
小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.
小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题:
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_关系时,仍有EF=BE+DF;
(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.
如图,AB是⊙O的直径,点E是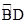 上一点,∠DAC=∠AED.
上一点,∠DAC=∠AED.
(1)求证:AC是⊙O的切线;
(2) 若点E是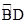 的中点,连结AE交BC于点F,当BD=5, CD=4时,求DF的值.
的中点,连结AE交BC于点F,当BD=5, CD=4时,求DF的值.
某中学以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.