已知函数f(x)=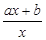 ex,a,b
ex,a,b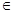 R,且a>0.
R,且a>0.
(1)若a=2,b=1,求函数f(x)的极值;
(2)设g(x)=a (x-1)ex-f(x).当a=1时,对任意x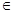 (0,+∞),都有g(x)≥1成立,求b的最大值;
(0,+∞),都有g(x)≥1成立,求b的最大值;
已知定义在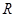 上的函数
上的函数
(1)判断并证明函数 的单调性;
的单调性;
(2)若 是奇函数,求
是奇函数,求 的值;
的值;
(3)若 的值域为D,且
的值域为D,且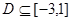 ,求
,求 的取值范围.
的取值范围.
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图1所示的一条折线表示,西红柿的种植成本与上市时间的关系用图2所示的抛物线表示。(注:市场售价和种植成本的单位:元/kg,时间单位:天)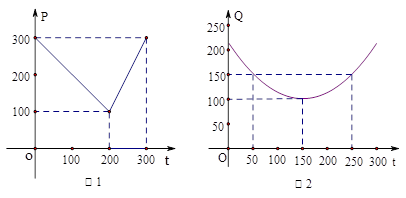
(1)写出图1表示的市场售价与时间的函数关系式 ;写出图2表示的种植成本与时间的函数关系式
;写出图2表示的种植成本与时间的函数关系式 ;
;
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?为多少?
已知集合 ,
,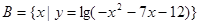 ,
,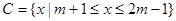 .
.
(1)求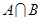 ;
;
(2)若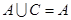 ,求实数
,求实数 的取值范围.
的取值范围.
设全集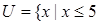 且
且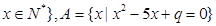 ,
,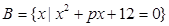 且
且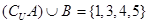 ,求实数
,求实数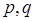 的值.
的值.
设数列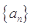 的前n项和为
的前n项和为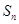 ,且
,且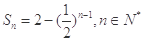 。
。
(Ⅰ)求数列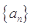 的通项公式;
的通项公式;
(Ⅱ)设数列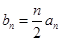 求数列
求数列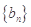 的前n项和
的前n项和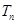 ;
;