如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx-k的图象的交点坐标为A(m,2).
(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx-k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx-k的值大于函数y=x的值的自变量x的取值范围. 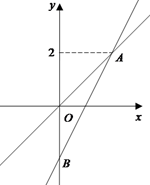
在计算器上,按照下面的程序进行操作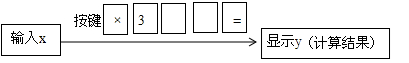
下表中的x与y分别是输入的6个数及相应的计算结果:上面操作程序中所按的第三个键和第四个键应是______.
| x |
﹣2 |
﹣1 |
0 |
1 |
2 |
3 |
| y |
﹣5 |
﹣2 |
1 |
4 |
7 |
10 |
(1)计算下列各题:
①22×32与(2×3)2;
②(﹣2)4×34与(﹣2×3)4;
③27×2与28.
(2)比较(1)中的结果,由此可以推断an×bn______(a×b)n,an+1_______an×a.
(3)试根据(2)的结论,不用计算器计算0.1252010×82011的值.
用计算器计算(写出按键顺序).
(1)(﹣15)3÷52
(2)﹣10+8÷22﹣(﹣4)×(﹣3).
有一张厚度是0.1mm的纸,假设我们能将它连续对折30次,这时它的厚度能超过珠穆朗玛峰的海拔高度(8845米)吗?请用计数器帮你得出答案.
一种圆柱体工件的底面半径是12cm,体积为9950cm2,它的高应做成多少?(π取3.14,结果精确到0.1,列式后可用计算器计算)