为了解“节约用水”活动开展一个月来的成效,某单位随机调查了20名职工家庭一个月来的节约用水情况,如下表所示:
| 节约水量(吨) |
0.5 |
1 |
1.5 |
2 |
| 职工数(人) |
10 |
5 |
4 |
1 |
请你根据上表提供的信息估计该单位100位职工的家庭一个月大约能节约用水多少吨?
如图,抛物线 的顶点为D(﹣1,4),与
的顶点为D(﹣1,4),与 轴交于点C(0,3),与
轴交于点C(0,3),与 轴交于A,B两点(点A在点B的左侧)。
轴交于A,B两点(点A在点B的左侧)。
(1)求抛物线的解析式;
(2)连接AC,CD,AD,试证明△ACD为直角三角形;
(3)若点E在抛物线上,EF⊥x轴于点F,以A、E、F为顶点的三角形与△ACD相似,试求出所有满足条件的点E的坐标。
某山区的一种特产由于运输原因,长期只能在当地销售,当地政府对该特产的销售投资收益为:每投入x万元,可获得利润P=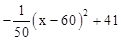 (万元)。当地政府拟规划加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出60万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售。在外地销售的投资收益为:每投入
(万元)。当地政府拟规划加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出60万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售。在外地销售的投资收益为:每投入 万元,可获利润Q=
万元,可获利润Q=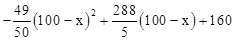 (万元)。
(万元)。
(1)若不进行开发,求5年所获利润的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)、(2),该方案是否具有实施价值?
如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式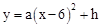 。已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
。已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。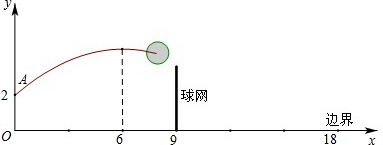
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围);
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求二次函数中二次项系数a的最大值。
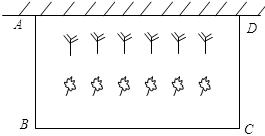
在青岛市开展的创城活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园 ,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的
,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的 (m),花园的面积为
(m),花园的面积为 (m
(m ).
).
(1)求 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)满足条件的花园面积能达到200
 吗?若能,求出此时
吗?若能,求出此时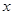 的值;若不能,说明理由;
的值;若不能,说明理由;
(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当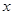 取何值时,花园的面积最大?最大面积为多少?
取何值时,花园的面积最大?最大面积为多少?
如图,已知一次函数 的图象交反比例函数
的图象交反比例函数 的图象于点A.B,交
的图象于点A.B,交 轴于点C。
轴于点C。
(1)求 的取值范围;
的取值范围;
(2)若点A的坐标是(2,4),且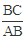 =
=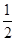 ,求
,求 的值和一次函数的解析式。
的值和一次函数的解析式。