设F1，F2分别是椭圆C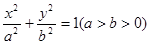：的左、右焦点．（1）设点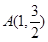是椭圆C上-优题课

题文

设F₁，F₂分别是椭圆C：的左、右焦点．
（1）设点是椭圆C上的点，且F₁（﹣1，0），F₂（1，0），试写出椭圆C的方程；
（2）设K是（1）中所得椭圆上的动点，求线段的中点B的轨迹方程；
（3）设点P是椭圆C上的任意一点，过原点的直线L与椭圆相交于M、N两点，若直线PM，PN的斜率都存在，并记为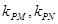，试探究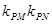的值是否与点P及直线L有关，并证明你的结论．

科目数学题型解答题难度困难

登录免费查看答案和解析

相关试题

（本小题满分13分）某企业准备招聘一批大学生到本单位就业，但在签约前要对他们的某项专业技能进行测试。在待测试的某一个小组中有男、女生共10人（其中女生人数多于男生人数），如果从中随机选2人参加测试，其中恰为一男一女的概率为（I）求该小组中女生的人数；（II）假设此项专业技能测试对该小组的学生而言，每个女生通过的概率均为，每个男生通过的概率均为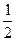，现对该小组中男生甲、男生乙和女生丙3个人进行测试，记这3人中通过测试的人数为随机变量，求的分布列和数学期望。

（本小题满分13分）
如图，已知正方形ABCD和梯形ACEF所在的平面互相垂直，
，CE//AF，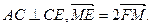
（I）求证：CM//平面BDF；
（II）求异面直线CM与FD所成角的大小；
（III）求二面角A—DF—B的大小。

（本小题满分13分）
已知点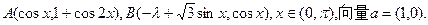
（I）若向量的值；（II）若向量的取值范围。

（本小题满分12分）已知函数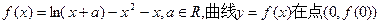处的切线恰好为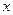轴。（I）求的值；（II）若区间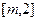恒为函数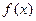的一个单调区间，求实数的最小值；（III）记（其中），的导函数，则函数是否存在极值点？若存在，请找出极值点并论证是极大值点还是极小值点；若不存在，请说明理由。

对于正整数 $n ⩾ 2$ ，用 $T_{n}$ 表示关于 $x$ 的一元二次方程 $x^{2} + 2 a x + b = 0$ 有实数根的有序数组 $(a, b)$ 的组数，其中 $a, b \in {1, 2, \dots, n}$ （ $a$ 和 $b$ 可以相等）；对于随机选取的 $a, b \in {1, 2, \dots, n}$ （ $a$ 和 $b$ 可以相等），记 $P_{n}$ 为关于 $x$ 的一元二次方程 $x^{2} + 2 a x + b = 0$ 有实数根的概率.
（1）求 $T_{n^{2}}$ 和 $P_{n^{2}}$ ；
（2）求证：对任意正整数 $n ⩾ 2$ ，有 $P_{n} > 1 - \frac{1}{\sqrt{n}}$ 。

试卷网试题网古诗词网作文网范文网