设函数 (m>0)
(m>0)
(1)证明:f(x)≥4;
(2)若f(2)>5,求m的取值范围.
已知公差不为0的等差数列 满足
满足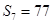 ,且
,且 ,
, ,
, 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
(本小题满分14分)已知函数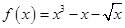
(1)判断 的单调性;
的单调性;
(2)求函数 的零点的个数;
的零点的个数;
(3)令 ,若函数
,若函数 在
在 内有极值,求实数
内有极值,求实数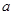 的取值范围。
的取值范围。
(本小题满分14分)如图,在平面直角坐标系 中,椭圆
中,椭圆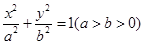 的离心率为
的离心率为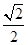 ,过椭圆右焦点F作两条互相垂直的弦
,过椭圆右焦点F作两条互相垂直的弦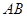 和
和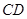 ,当直线
,当直线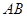 斜率为0时,
斜率为0时,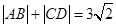
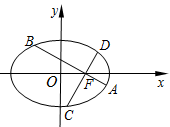
(1)求椭圆的方程;
(2)求由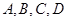 四点构成的四边形的面积的取值范围。
四点构成的四边形的面积的取值范围。
(本小题满分13分)已知等比数列 的公比
的公比 ,前n项和为
,前n项和为 且
且 成等差数列,数列
成等差数列,数列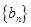 的前n项和为
的前n项和为 ,其中
,其中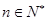 。
。
(1)求数列 的通项公式;
的通项公式;
(2)求数列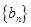 的通项公式;
的通项公式;
(3)设 ,
, ,求集合
,求集合 中的所有元素之和。
中的所有元素之和。
(本小题满分12分)正方体 的棱长为1,点
的棱长为1,点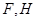 封闭为
封闭为 的中点。
的中点。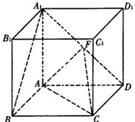
(1)证明: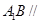 平面
平面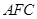 ;
;
(2)证明: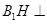 平面
平面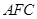 。
。