.如果{an}为递增数列,则{an}的通项公式可以为( ).
A.an=-2n+3 B.an=-n2-3n+1 C.an= an=1+log2 n
an=1+log2 n
平面上有四点,连结其中的两点的一切直线中的任何两条直线不重合、不平行、不垂直,从每一点出发,向其他三点作成的一切直线作垂线,则这些垂线的交点个数最多为
| A.66 | B.60 | C.52 | D.44 |
设直线系 ,则下列命题中是真命题的个数是
,则下列命题中是真命题的个数是
①存在一个圆与所有直线相交
②存在一个圆与所有直线不相交 ③存在一个圆与所有直线相切
④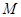 中所有直线均经过一个定点 ⑤存在定点
中所有直线均经过一个定点 ⑤存在定点 不在
不在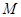 中的任一条直线上
中的任一条直线上
⑥对于任意整数 ,存在正
,存在正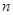 边形,其所有边均在
边形,其所有边均在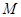 中的直线上
中的直线上
⑦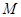 中的直线所能围成的正三角形面积都相等
中的直线所能围成的正三角形面积都相等
| A.3 | B.4 | C.5 | D.6 |
已知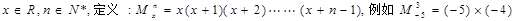
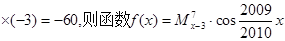
| A.是偶函数不是奇函数 | B.是奇函数不是偶函数 |
| C.既是奇函数又是偶函数 | D.既不是奇函数又不是偶函数 |
“数列 为等比数列”是“数列
为等比数列”是“数列 为等比数列”的
为等比数列”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下面说法正确的是
A.若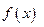 在 在 处存在极限,则 处存在极限,则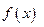 在 在 处连续 处连续 |
B.若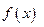 在 在 处无定义,则 处无定义,则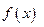 在 在 处无极限 处无极限 |
C.若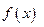 在 在 处连续,则 处连续,则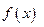 在 在 处存在极限 处存在极限 |
D.若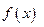 在 在 处连续,则 处连续,则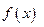 在 在 处可导 处可导 |