已知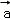 ,
,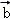 ,
,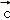 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中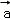 =(1,2)
=(1,2)
(1)若|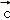 |=2
|=2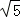 ,
,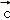 ∥
∥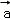 ,求
,求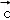 的坐标及
的坐标及 ;
;
(2)若|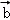 |=
|=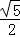 ,且
,且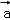 +2
+2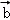 与3
与3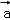 ﹣
﹣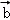 垂直,求
垂直,求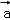 与
与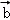 的夹角.
的夹角.
(本小题满分12分)已知函数
 ,函数
,函数
⑴当 时,求函数
时,求函数 的表达式;
的表达式;
⑵若 ,函数
,函数 在
在 上的最小值是2 ,求
上的最小值是2 ,求 的值;
的值;
⑶在⑵的条件下,求直线 与函数
与函数 的图象所围成图形的面积.
的图象所围成图形的面积.
(本小题满分12分)设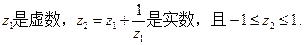
(1)求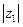 的值以及
的值以及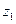 的实部的取值范围;
的实部的取值范围;
(2)若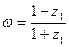 ,求证:
,求证: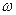 为纯虚数.
为纯虚数.
(本小题12分)已知数列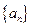 满足
满足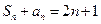 ,
,
(1) 写出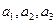 并推测
并推测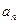 的表达式;
的表达式;
(2) 用数学归纳法证明所得的结论.
(本小题满分12分)如图,点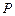 为斜三棱柱
为斜三棱柱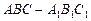 的侧棱
的侧棱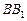 上一点
上一点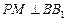 交
交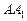 于点
于点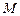 ,
,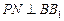 交
交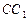 于点
于点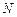 .在任意
.在任意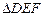 中有余弦定理:
中有余弦定理: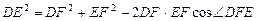 .拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式.
.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式.
(本小题12分)定义在定义域D内的函数 ,若对任意的
,若对任意的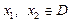 都有
都有 ,则称函数
,则称函数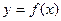 为“妈祖函数”,否则称“非妈祖函数”.试问函数
为“妈祖函数”,否则称“非妈祖函数”.试问函数 ,
,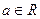 )是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
)是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.

