已知圆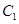
的参数方程为
（
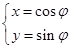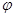为参数），以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系，圆
的极坐标方程为
．
（1）将圆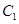的参数方程化为普通方程，将圆的极坐标方程化为直角坐标方程；
（2）圆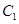,是否相交，若相交，请求出公共弦的长；若不相交，请说明理由．
为了了
解高一学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如下图），图中从左到右各小长方形面积之比为2:4:17:15:9:3，第二小组频数为12.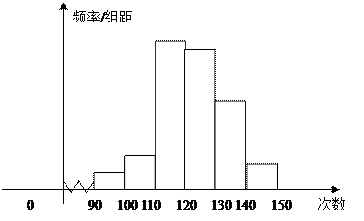
（1）第二小组的频率是多少？样本容量是多少？
（2）若次数
在110以上（含110次）为达标，试估计该学校全体高一的学生达标的概率
（3）为了分析学生的体能与身高，体重
等方面的关系，必须再从样本中按分层抽样方法抽出50人作进一步分析，则体能在[120，130）的这段应抽多少人?
（1）化简：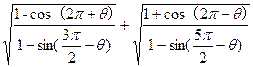
（2）求值：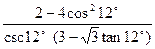
在以O为原点的直角坐标系中，点A（4，－3）为△OAB的直角顶点.已知|AB|=2|OA|，且点B的纵坐标大于零.
（1）求向量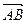
的坐标；
（2）求圆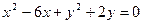
关于直线OB对称的圆的方程；
（3）是否存在实数a，使函数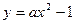
的图像上总有关于直线OB对称的两个点？若不存在，说明理由：若存在，求a的取值范围.
(题满分12) 已知
（1）化简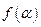
；（2）若
，求
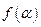的值．[
( (本小题满分10分)已知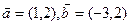
①若
与
垂直，
求k的值
②若与平行，求k的值