某中学社团部志愿者协会共有6名男同学,4名女同学. 在这10名同学中,3名同学来自动漫社,其余7名同学来自摄影社、话剧社等其他互不相同的七个社团. 现从这10名同学中随机选取3名同学,到社区参加志愿活动(每位同学被选到的可能性相同).
(Ⅰ)求选出的3名同学是来自互不相同社团的概率;
(Ⅱ)设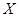 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量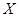 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知函数
(Ⅰ)求函数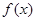 的对称中心;
的对称中心;
(Ⅱ)已知△ABC内角 的对边分别为
的对边分别为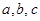 ,且
,且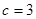 ,
,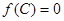 ,
,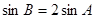 ,求
,求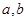
(本小题满分14分)已知椭圆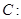
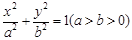 的右焦点为
的右焦点为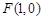 ,且点
,且点 在椭圆
在椭圆 上,
上,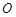 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设过定点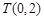 的直线
的直线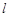 与椭圆
与椭圆 交于不同的两点
交于不同的两点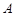 、
、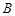 ,且
,且 为锐角,求直线
为锐角,求直线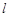 的斜率
的斜率 的取值范围;
的取值范围;
(Ⅲ)过椭圆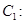
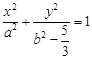 上异于其顶点的任一点
上异于其顶点的任一点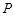 ,作圆
,作圆
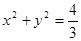 的两条切线,切点分别为
的两条切线,切点分别为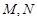 (
(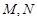 不在坐标轴上),若直线
不在坐标轴上),若直线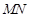 在
在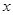 轴、
轴、 轴上的截距分别为
轴上的截距分别为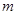 、
、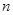 ,证明:
,证明: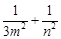 为定值.
为定值.
(本小题满分13分)设函数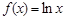 ,
, ,函数
,函数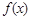 的图象与
的图象与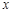 轴的交点在函数
轴的交点在函数 的图象上,且在此点处两曲线有相同的切线.
的图象上,且在此点处两曲线有相同的切线.
(Ⅰ) 求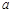 、
、 的值;
的值;
(Ⅱ) 设定义在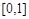 上的函数
上的函数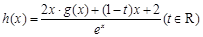 的最大值为
的最大值为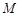 ,最小值为
,最小值为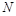 ,且
,且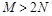 ,求实数
,求实数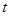 的取值范围.
的取值范围.
(本小题满分12分)已知数列 是等比数列,首项
是等比数列,首项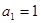 ,公比
,公比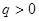 ,其前
,其前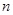 项和为
项和为 ,且
,且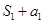 ,
, ,
,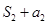 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)若数列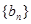 满足
满足 ,
,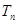 为数列
为数列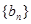 的前
的前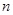 项和,若
项和,若 恒成立,求
恒成立,求 的最大值.
的最大值.
(本小题满分12分)如图所示,已知在四棱锥 中,
中, 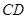 ∥
∥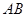 ,
, ,
,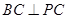 ,且
,且

(1)求证: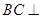 平面
平面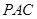 ;
;
(2)试在线段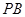 上找一点
上找一点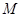 ,使
,使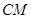 ∥平面
∥平面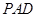 , 并说明理由;
, 并说明理由;
(3)若点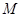 是由(2)中确定的,且
是由(2)中确定的,且 ,求四面体
,求四面体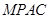 的体积.
的体积.