如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A，B，直线CD与x轴、y轴分别交于点C，D，AB与CD相交于点E，线段OA，OC的长是一元二次方程x2﹣18x+72=0的两根（OA＞OC），BE=5，tan∠ABO=
．
（1）求点A，C的坐标；
（2）若反比例函数y=
的图象经过点E，求k的值；
（3）若点P在坐标轴上，在平面内是否存在一点Q，使以点C，E，P，Q为顶点的四边形是矩形？若存在，请写出满足条件的点Q的个数，并直接写出位于x轴下方的点Q的坐标；若不存在，请说明理由．
（本题6分） 如图，在△ABC中，∠ACB=90，AC=BC．直线L经过点C且绕点C转动，分别过点A、B向直线DE引垂线，垂足分别为点D、E．
求证：AD+BE=DE．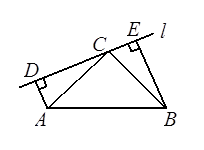
（本题6分）如图，点E、C在线段BF上，BE=CF，AB∥DE，∠ACB=∠F，那么△ABC与△DEF全等吗?为什么?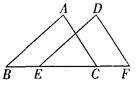
（本题6分）下列图形是否是轴对称图形，画出轴对称图形的所有对称轴．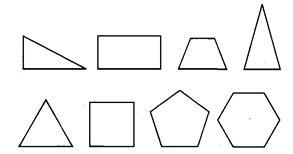
思考：正三角形有_______条对称轴；正四边形有______条对称轴；正五边形有_______条对称轴；正六边形有_______条对称轴；正n边形有_______条对称轴．
当n越来越大时，正多边形接近于什么图形？它有多少条对称轴？
（本题6分）你能把如图①所示的长方形分成2个全等图形吗?把如图②所示的三角形分成3个全等三角形吗?把如图③所示的长方形分成4个全等三角形吗?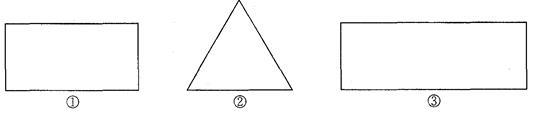
（本题3分）如图，在网格纸上，画出所给图形关于直线l对称的图形．