如图,在边长为1的正方形组成的网格中, 的顶点均在格点上,其中点
的顶点均在格点上,其中点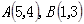 ,将
,将 绕点
绕点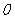 逆时针旋转
逆时针旋转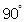 后得到
后得到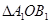 .
.
(1)画出 ;
;
(2)在旋转过程中点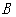 所经过的路径长为 ;
所经过的路径长为 ;
(3)求在旋转过程中线段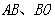 扫过的图形的面积之和.
扫过的图形的面积之和.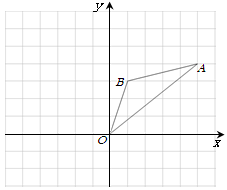
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.
供选择的三个条件(请从其中选择一个):
①AB=ED;
②BC=EF;
③∠ACB=∠DFE.
如图,在正方形网格中,△OBC的顶点分别为O(0,0), B(3,-1)、C(2,1).
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′ ,画出△OB′C′,并写出点B′、C′的坐标:B′(,),C′(,);
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标(,).
先化简,再求值: ,其中
,其中 .
.
解方程:
解不等式组 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.