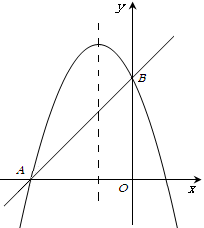
如图,抛物线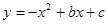 交
交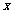 轴于点
轴于点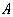 ,交
,交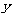 轴于点
轴于点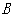 ,已知经过点
,已知经过点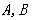 的直线的表达式为
的直线的表达式为 .
.
(1)求抛物线的函数表达式及其顶点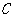 的坐标;
的坐标;
(2)如图①,点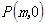 是线段
是线段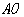 上的一个动点,其中
上的一个动点,其中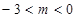 ,作直线
,作直线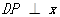 轴,交直线
轴,交直线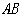 于
于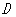 ,交抛物线于
,交抛物线于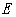 ,作
,作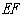 ∥
∥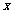 轴,交直线
轴,交直线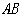 于点
于点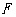 ,四边形
,四边形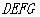 为矩形.设矩形
为矩形.设矩形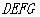 的周长为
的周长为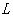 ,写出
,写出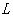 与
与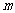 的函数关系式,并求
的函数关系式,并求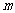 为何值时周长
为何值时周长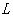 最大;
最大;
(3)如图②,在抛物线的对称轴上是否存在点 ,使点
,使点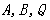 构成的三角形是以
构成的三角形是以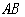 为腰的等腰三角形.若存在,直接写出所有符合条件的点
为腰的等腰三角形.若存在,直接写出所有符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.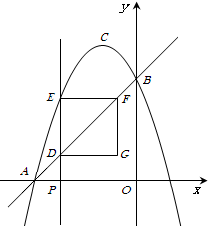
图① 图②
如图,在平面直角坐标系xoy中,E(8,0),F(0 , 6).
(1)当G(4,8)时,则∠FGE=°
(2)在图中的网格区域内找一点P,使∠FPE=90°且四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形.
要求:写出点P点坐标,画出过P点的分割线并指出分割线(不必说明理由,不写画法).
已知:如图, AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,联结OD , 作BE∥OD交⊙O于点E, 联结DE并延长交BN于点C.
(1)求证:DC是⊙O的切线;
(2)若AD=l,BC=4,求直径AB的长. 
某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树的棵树和所占百分比情况进行了调查,将收集的数据整理并绘制成图1和图2两幅不完整的统计图,请根据图中的信息,完成下列问题:
(1)这四个班共植树 棵;
(2)请补全两幅统计图;
(3)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树大约有多少棵?
已知:如图,正方形ABCD中,点E为AD边的中点,联结CE.
求cos∠ACE和tan∠ACE的值.
列方程(组)解应用题:
某工厂现在平均每天比原计划平均每天多生产50台机器,现在生产600台机器所需的时间与原计划生产400台机器所需的时间相同,现在平均每天生产多少台机器?