如图所示,水平地面上静止放置一辆小车A,质量mA=4kg,车长l=0.4m,上表面不光滑,小车与地面间的摩擦力极小,可以忽略不计。小车以v=1.2m/s在水平地面匀速运动。将可视为质点的物块B无初速度地置于A的最右端,B的质量mB=2kg,A、B间的动摩擦因素为μ=0.2,AB间的最大静摩擦力可以认为等于滑动摩擦力。现对A施加一个水平向右的恒力F作用。(g=10m/s2,所有计算结果保留两位有效数字)
(1).要维持小车匀速运动,求F的大小?
(2).当A匀速运动时,求从B放上A至B相对A静止,A发生的位移大小?
(3)要使物块B不从小车A上掉下,求F的大小?
.一辆汽车在十字路口等候绿灯,当绿灯亮时汽车开始匀加速行驶,汽车的牵引力保持为车重的0.6倍,汽车行驶时所受阻力为车重的0.3倍,恰在这时一辆自行车以6m/s的速度匀速从后面超过汽车,则:
(1)汽车从路口启动后,在追上自行车之前经多长时间两车相距最远,距离多少?
(2)若该路段汽车最大速度不允许超过9m/s,则汽车开始运动后经多长时间追上自行车?
如图所示,弹簧AB原长为35cm,A端挂一个重50N的物体,手执B端,将物体置于倾角为30°的斜面上。当物体沿斜面匀速下滑时,弹簧长度为40cm;当物体匀速上滑时,弹簧长度为50cm,求:
(1)在图A和图B中分别画出物体下滑和上滑时的受力图
(2)弹簧的劲度系数
(3)物体与斜面的动摩擦因数

如图,一重为10N的物体静放在水平地面上,现对它施加一大小为F=4N的水平向右拉力,求:(g=10m/s2,物体与地面间动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力)
(1)物体所受的摩擦力的大小和方向
(2)物体的加速度大小
物体做匀加速直线运动的初速度v0=2m/s,加速度a=1m/s2,试求:
(1)物体在第5s末的速度是多大?
(2)物体在前5s内通过的位移多大?
如图所示,水平传送带以不变的速度v向右运动,将工件轻轻放在传送带的左端,由于摩擦力的作用,工件做匀加速运动,经过时间t,速度变为v;再经时间2t,工件到达传送带的右端,求: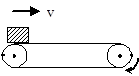
(1)工件在水平传送带上滑动时的加速度
(2)工件与水平传送带间的动摩擦因数
(3)工件从水平传送带的左端到达右端通过的距离