小张骑车往返于甲、乙两地，距甲地的路程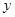
（千米）与时间
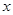（小时）的函数图象如图所示．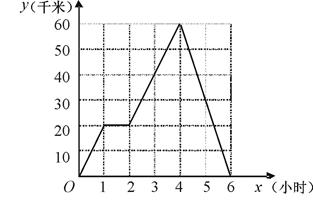
（1）小张在路上停留 小时，他从乙地返回时骑车的速度为 千米／时．
（2）小王与小张同时出发，按相同路线前往乙地，距甲地的路程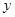（千米）与时间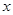（小时）的函数关系式为
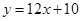．小王与小张在途中共相遇几次？请你计算第一次相遇的时间．
如图，抛物线y=
x2-mx+n与x轴交于A、B两点，与y轴交于点C（0，-1）．且对称轴x=l．
（1）求出抛物线的解析式及A、B两点的坐标；
（2）在x轴下方的抛物线上是否存在点D，使四边形ABDC的面积为3？若存在，求出点D的坐标；若不存在．说明理由（使用图1）；
（3）点Q在y轴上，点P在抛物线上，要使Q、P、A、B为顶点的四边形是平行四边形，请求出所有满足条件的点P的坐标（使用图2）．
如图，已知正方形ABCD，点E是边AB上一点，点O是线段AE上的一个动点（不与A、E重合），以O为圆心，OB为半径的圆与边AD相交于点M，过点M作⊙O的切线交DC于点N，连结OM、ON、BM、BN．
（1）求证：△AOM∽△DMN；
（2）求∠MBN的度数．
已知矩形OABC中，OA=3，AB=6，以OA、OC所在的直线为坐标轴，建立如图所示的平面直角坐标系．将矩形OABC绕点O顺时针方向旋转，得到矩形ODEF，当点B在直线DE上时，设直线DE和x轴交于点P，与y轴交于点Q．
（1）求证：△BCQ≌△ODQ；
（2）求点P的坐标．
某工厂生产的某种产品按质量分为10个档次，第1档次（最低档次）的产品一天能生产95件，每件利润6元．每提2014-2015学年高一个档次，每件利润增加2元，但一天产量减少5件．
（1）若生产第x档次的产品一天的总利润为y元（其中x为正整数，且1≤x≤10），求出y关于x的函数关系式；
（2）若生产第x档次的产品一天的总利润为1120元，求该产品的质量档次．
如图，在东西方向的海岸线MN上有相距10海里的A、B两艘船，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东60°方向上，船P在船B的北偏西45°方向上．求船P到海岸线MN的距离（结果保留根号）．