某产品的广告费用与销售额的统计数据如下表
根据上表可得回归方程
中的
为9．4，据此模型预报广告费用为6万元时
销售额为 （）
| A．63.6万元 | B．65.5万元 | C．67.7万元 | D．72.0万元 |
通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如下的列联表：
| 男 |
女 |
总计 |
|
| 走天桥 |
40 |
20 |
60 |
| 走斑马线 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由
，算得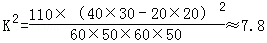
参照独立性检验附表，得到的正确结论是（）
A.有99%的把握认为“选择过马路的方式与性别有关”
B.有99%的把握认为“选择过马路的方式与性别无关”
C.在犯错误的概率不超过0.1%的前提下，认为“选择过马路的方式与性别有关”
D.在犯错误的概率不超过0.1%的前提下，认为“选择过马路的方式与性别无关”
为了普及环保知识，增强环保意识，某大学从理工类专业的A班和文史类专业的B班各抽取20名同学参加环保知识测试．统计得到成绩与专业的列联表：
| 优秀 |
非优秀 |
总计 |
|
| A班 |
14 |
6 |
20 |
| B班 |
7 |
13 |
20 |
| C班 |
21 |
19 |
40 |
附：参考公式及数据：
（1）卡方统计量
（其中n=n11+n12+n21+n22）；
（2）独立性检验的临界值表：
| P（x2≥k0） |
0.050 |
0.010 |
| K0 |
3.841 |
6.635 |
则下列说法正确的是（）
A.有99%的把握认为环保知识测试成绩与专业有关
B.有99%的把握认为环保知识测试成绩与专业无关
C.有95%的把握认为环保知识测试成绩与专业有关
D.有95%的把握认为环保知识测试成绩与专业无关
在调查学生数学成绩与物理成绩之间的关系时，得到如下数据（人数：）
| 物理成绩好 |
物理成绩不好 |
合计 |
|
| 数学成绩好 |
18 |
7 |
25 |
| 数学成绩不好 |
6 |
19 |
25 |
| 合计 |
24 |
26 |
50 |
数学成绩与物理成绩之间有把握有关？（）
A.90% B.95% C.97.5% D.99%
某校为了研究学生的性别和对待某一活动的态度（支持和不支持两种态度）的关系，运用2×2列联表进行独立性检验，经计算K2=7.069，则所得到的统计学结论是：有（）的把握认为“学生性别与支持该活动有关系”．
| P（k2≥k0） |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
| k0 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
A.0.1% B.1% C.99% D.99.9%
下列说法：
①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；
②设有一个回归方程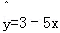
，变量x增加一个单位时，y平均增加5个单位；
③线性回归方程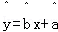
必过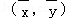
；
④在一个2×2列联表中，由计算得K2=13.079，则有99%的把握确认这两个变量间有关系；
其中错误的个数是（）
| A．0 | B．1 | C．2 | D．3 |