已知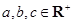 ,证明:
,证明:
(Ⅰ)(A + b + c )(A2 + b2 + c2 ) ≤ 3(A3 + b3 +c3 );
(Ⅱ) .
.
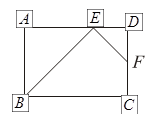
如图,在矩形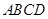 中,点
中,点 为边
为边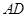 上的点,点
上的点,点 为边
为边 的中点,
的中点, 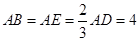 ,现将
,现将 沿
沿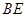 边折至
边折至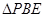 位置,且平面
位置,且平面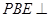 平面
平面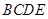 .
.
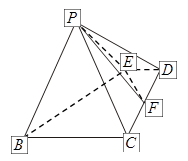
(Ⅰ)求证:平面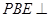 平面
平面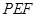 ;
;
(Ⅱ)求四棱锥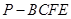 的体积.
的体积.
(本小题满分15分)已知△ABC中的三个内角A,B,C所对的边分别为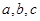 ,且满足
,且满足
(Ⅰ)求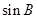 ;(Ⅱ)求△ABC的面积.
;(Ⅱ)求△ABC的面积.
(原创)已知{ }是公比为q(q≠1)的等比数列,且存在m∈
}是公比为q(q≠1)的等比数列,且存在m∈ 使得
使得 成等差数列.
成等差数列.
(1)求q的值;
(2)若 =1,
=1, 数列{
数列{ }前n项和为
}前n项和为 ,求
,求 .
.
(本小题满分13分)已知椭圆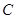 的两个焦点的坐标分别为
的两个焦点的坐标分别为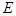
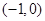 ,
,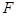
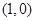 ,并且经过点(
,并且经过点(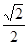 ,
,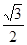 ),M、N为椭圆
),M、N为椭圆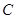 上关于
上关于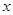 轴对称的不同两点.
轴对称的不同两点.
(1)求椭圆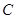 的标准方程;
的标准方程;
(2)若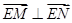 ,试求点
,试求点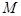 的坐标;
的坐标;
(3)若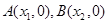 为
为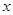 轴上两点,且
轴上两点,且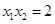 ,试判断直线
,试判断直线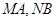 的交点
的交点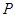 是否在椭圆
是否在椭圆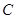 上,并证明你的结论.
上,并证明你的结论.
【改编题】(本大题满分13分)设函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)  时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)函数 是
是 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值.
上的最小值.
(Ⅲ)函数 在区间
在区间 内有零点,证明:
内有零点,证明: .
.