【改编题】(本大题满分13分)设函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)  时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)函数 是
是 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值.
上的最小值.
(Ⅲ)函数 在区间
在区间 内有零点,证明:
内有零点,证明: .
.
已知数列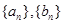 满足:
满足: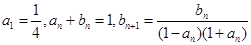 .
.
(Ⅰ)求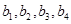 ;
;
(Ⅱ)设 ,求数列
,求数列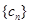 的通项公式;
的通项公式;
(Ⅲ)设 ,不等式
,不等式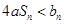 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.
已知向量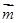
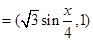 ,
,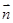
 ,函数
,函数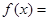
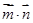
(Ⅰ)若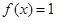 ,求
,求 的值;
的值;
(Ⅱ)在锐角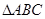 中,角
中,角 的对边分别是
的对边分别是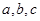 ,且满足
,且满足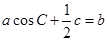 ,求
,求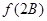 的取值范围.
的取值范围.
某中学的高二(1)班男同学有 名,女同学有
名,女同学有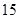 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个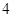 人的课外兴趣小组.
人的课外兴趣小组.
(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实 验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实 验,求选出的两名同学中恰有一名女同学的概率;
已知函数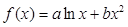 图象上点
图象上点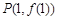 处的切线方程为
处的切线方程为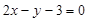 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)函数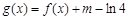 ,若方程
,若方程 在
在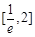 上恰有两解,求实数
上恰有两解,求实数 的取值范围
的取值范围
已知点 是离心率为
是离心率为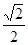 的椭圆C:
的椭圆C: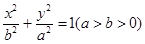 上的一点。斜率为
上的一点。斜率为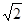 直线BD交椭圆C于B、D两点,且A、B、D三点不重合。
直线BD交椭圆C于B、D两点,且A、B、D三点不重合。
(Ⅰ)求椭圆C的方程;
(Ⅱ) 面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?