2014年巴西世界杯足球赛正在如火如荼的进行，小明和喜爱足球的伙伴们一起预测“巴西队”能否获得本届杯赛的冠军，他们分别在3月、4月、5月、6月进行了四次预测，并且每次参加预测的人数相同，小明根据四次预测结果绘制成如下两幅不完整的统计图．请你根据图中提供的信息解答下列问题：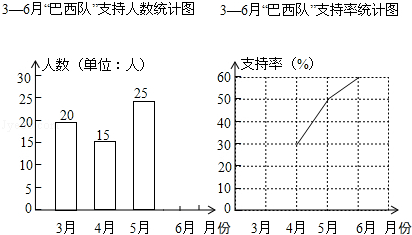
（1）每次有 人参加预测；
（2）计算6月份预测“巴西队”夺冠的人数；
（3）补全条形统计图和折线统计图．
已知：如图，C是AE的中点，∠B=∠D，BC∥DE．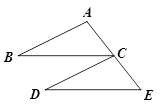
求证：AB=CD
解不等式
＜
，并把它的解集在数轴上表示出来.
如图，在平面直角坐标系中，点C（-3,0），点A、B分别在x轴，y轴的正半轴上，且满足
.求点A、B坐标
若点P从点C出发，以每秒1个单位的速度沿射线CB运动，连接AP。设△ABP面积为S，点P的运动时间为t秒，求S与t的函数关系式，并写出自变量的取值范围
在（2）的条件下，是否存在点P，使以点A、B、P为顶点的三角形与△AOB相似？若存在，请直接写出点P的坐标；若不存在，请说明理由。
如图，在△ABC中，高BD、CE相交于点O.
试说明：
；试说明：△AED∽△ACB
试说明：△DOE与△COB相似。
某一工程，在工程招标时接到甲、乙两个工程队的投标书．施工一天，需付甲工程队工程款1.2万元，乙工程队工程款0.5万元．工程领导小组根据甲、乙两队的投标书测算，有如下方案：甲队单独完成这项工程刚好如期完成；乙队单独完成这项工程要比规定日期多用6天；若甲、乙两队合做3天，余下的工程由乙队单独做也正好如期完成．
试问：在不耽误工期的前提下，你觉得哪一种施工方案最节省工程款？请说明理由．