如图,在直角坐标系 中,圆
中,圆 与
与 轴负半轴交于点
轴负半轴交于点 ,过点
,过点 的直线
的直线 ,
, 分别与圆
分别与圆 交于
交于 ,
, 两点.
两点.
(1)若 ,
, ,求△
,求△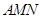 的面积;
的面积;
(2)过点 作圆O的两条切线,切点分别为E,F,求
作圆O的两条切线,切点分别为E,F,求 ;
;
(3)若 ,求证:直线
,求证:直线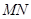 过定点.
过定点.
在直角坐标系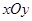 中,半圆C的参数方程为
中,半圆C的参数方程为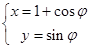 (
( 为参数,
为参数,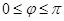 ),以O为极点,x轴的非负半轴为极轴建立极坐标系.
),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求C的极坐标方程;
(Ⅱ)直线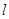 的极坐标方程是
的极坐标方程是 ,射线OM:
,射线OM: 与半圆C的交点为O、P,与直线
与半圆C的交点为O、P,与直线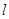 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
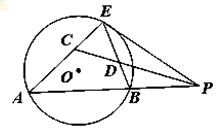
如图,已知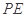 切⊙
切⊙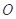 于点
于点 ,割线
,割线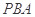 交⊙
交⊙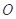 于
于 两点,∠
两点,∠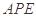 的平分线和
的平分线和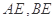 分别交于点
分别交于点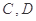 .
.
求证:(1)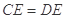 ;
;
(2)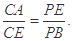
设函数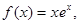
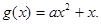 [K]
[K]
(1)若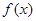 与
与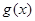 具有完全相同的单调区间,求
具有完全相同的单调区间,求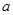 的值;
的值;
(2)若当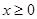 时恒有
时恒有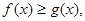 求
求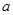 的取值范围.
的取值范围.
已知椭圆
 的焦距为
的焦距为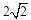 ,且过点
,且过点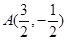 .
.
(1)求椭圆的方程;
(2)已知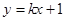 ,是否存在
,是否存在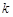 使得点
使得点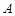 关于
关于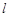 的对称点
的对称点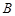 (不同于点
(不同于点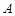 )在椭圆
)在椭圆 上?若存在求出此时直线
上?若存在求出此时直线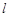 的方程,若不存在说明理由.
的方程,若不存在说明理由.
在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格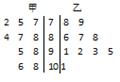
(1)用样本估计总体,请根据茎叶图对甲乙两个班级的成绩进行比较。
(2)求从甲班10名学生和乙班10名学生中各抽取一人,已知有人及格的条件下乙班同学不及格的概率;
(3)从甲班10人中抽取一人,乙班10人中抽取二人,三人中及格人数记为X,求X的分布列和期望。