已知椭圆C: +
+ =1(a>b>0)的下顶点为P(0,﹣1),P到焦点的距离为
=1(a>b>0)的下顶点为P(0,﹣1),P到焦点的距离为 .
.
(Ⅰ)设Q是椭圆上的动点,求|PQ|的最大值;
(Ⅱ)若直线l与圆O:x2+y2=1相切,并与椭圆C交于不同的两点A、B.当 •
• =λ,且满足
=λ,且满足 ≤λ≤
≤λ≤ 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
(本题10分)设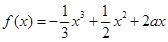 .若
.若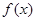 在
在 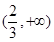 存在单调增区间,求a的取值范围.
存在单调增区间,求a的取值范围.
(本题8分) 已知直线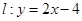 被抛物线C:
被抛物线C: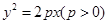 截得的弦长
截得的弦长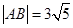 .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C的焦点为F,求三角形ABF的面积.
(本题8分) 设函数 定义在
定义在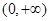 上,
上,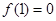 ,导函数
,导函数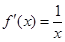 ,
,  .求
.求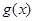 的单调区间和最小值.
的单调区间和最小值.
数列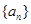 ,
,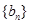 (
(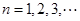 )由下列条件确定:①
)由下列条件确定:①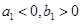 ;②当
;②当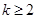 时,
时,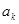 与
与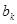 满足:当
满足:当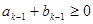 时,
时,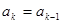 ,
,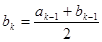 ;当
;当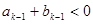 时,
时,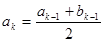 ,
,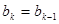 .
.
(Ⅰ)若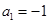 ,
,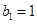 ,写出
,写出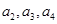 ,并求数列
,并求数列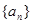 的通项公式;
的通项公式;
(Ⅱ)在数列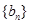 中,若
中,若 (
(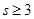 ,且
,且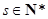 ),试用
),试用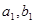 表示
表示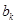
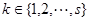 ;
;
(Ⅲ)在(Ⅰ)的条件下,设数列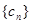
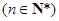 满足
满足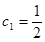 ,
,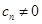 ,
,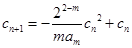 (其中
(其中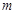 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当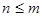 时,恒有
时,恒有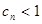 .
.
已知椭圆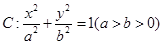 的离心率为
的离心率为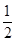 ,直线
,直线 过点
过点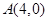 ,
,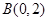 ,且与椭圆
,且与椭圆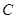 相切于点
相切于点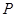 .
.
(Ⅰ)求椭圆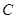 的方程;
的方程;
(Ⅱ)是否存在过点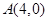 的直线
的直线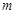 与椭圆
与椭圆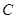 相交于不同的两点
相交于不同的两点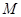 、
、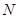 ,使得
,使得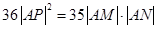 ?若存在,试求出直线
?若存在,试求出直线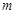 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.