为培养高中生综合实践能力和团队合作意识,某市教育部门主办了全市高中生综合实践知识与技能竞赛.该竞赛分为预赛和决赛两个阶段,参加决赛的团队按照抽签方式决定出场顺序.通过预赛,共选拔出甲、乙等六个优秀团队参加决赛.
(Ⅰ)求决赛出场的顺序中,甲不在第一位、乙不在第六位的概率;
(Ⅱ)若决赛中甲队和乙队之间间隔的团队数记为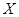 ,求
,求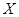 的分布列和数学期望.
的分布列和数学期望.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、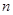 人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(1)求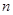 的值;
的值;
(2)把在前排就坐的高二代表队6人分别记为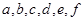 ,现随机从中抽取2人上台抽奖,求
,现随机从中抽取2人上台抽奖,求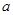 和
和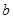 至少有一人上台抽奖的概率;
至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个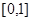 之间的均匀随机数
之间的均匀随机数 ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.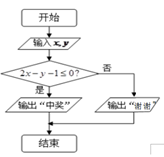
已知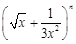 的第五项的二项式系数与第三项的二项式系数的比是
的第五项的二项式系数与第三项的二项式系数的比是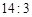 ,
,
(1)求n;
(2)求展开式中常数项.
从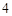 名男同学中选出
名男同学中选出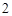 人,
人, 名女同学中选出
名女同学中选出 人,并将选出的
人,并将选出的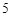 人排成一排.
人排成一排.
(1)共有多少种不同的排法?
(2)若选出的5人排队,男、女同学各排一排,共有多少种不同的排法?(用数字表示)
某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是: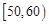 、
、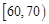 、
、 、
、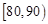 、
、 .
.
(1)求图中 的值;
的值;
(2)根据频率分布直方图,估计这200名学生物理成绩的平均值和中位数.
已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.
(1)若m=4,求直线l被圆C所截得弦长的最大值;
(2)若直线l是圆心下方的切线,当a在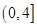 的变化时,求m的取值范围.
的变化时,求m的取值范围.