我市某校某数学老师这学期分别用 两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的数学期末考试成绩,分别为
两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的数学期末考试成绩,分别为
甲班: .
.
乙班: .
.
(Ⅰ)作出甲乙两班分别抽取的20名学生数学期末成绩的茎叶图,依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班所抽数学成绩不低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率.
实数m取什么值时,复平面内表示复数 的点
的点
(1)位于第四象限?(2)位于第一、三象限?(3)位于直线 上?
上?
已知抛物线 的一条焦点弦AB被焦点F分成长为m、n的两部分,求证:
的一条焦点弦AB被焦点F分成长为m、n的两部分,求证: 为定值
为定值
已知椭圆的中心在原点,准线为 如果直线
如果直线 与椭圆的交点在x轴上的射影恰为椭圆的焦点
与椭圆的交点在x轴上的射影恰为椭圆的焦点
(1)求椭圆方程
(2)求过左焦点F1且与直线 平行的弦EF的中点坐标
平行的弦EF的中点坐标
已知双曲线C以椭圆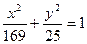 的焦点为顶点,顶点为焦点
的焦点为顶点,顶点为焦点
(1)求双曲线C的标准方程;
(2)若双曲线C的左、右两焦点分别为F1、F2,P为双曲线C左支上一点,若 求S△PF1F2
求S△PF1F2
某养殖场需要甲、乙两种饲料的混合物,甲中每两含蛋白质10克,脂肪0.5克和碳水化合物10克;乙中为5克、1克和10克,又甲、乙两种饲料价格分别为5分/两和4分/两,而要求甲、乙两种饲料混合后每份至少含蛋白质100克,脂肪10克和碳水化合物180克,问每份混合饲料中用甲、乙两种饲料各多少两,才能使成本最低?