某养殖场需要甲、乙两种饲料的混合物,甲中每两含蛋白质10克,脂肪0.5克和碳水化合物10克;乙中为5克、1克和10克,又甲、乙两种饲料价格分别为5分/两和4分/两,而要求甲、乙两种饲料混合后每份至少含蛋白质100克,脂肪10克和碳水化合物180克,问每份混合饲料中用甲、乙两种饲料各多少两,才能使成本最低?
 ,则称
,则称 为
为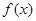 与
与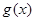
在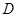 上的一个“分界函数”.如
上的一个“分界函数”.如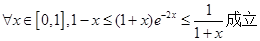 ,则称
,则称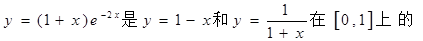 一个“分界函数”。
一个“分界函数”。
(1)求证: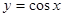 是
是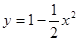 和
和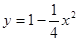 在
在 上的一个“分界函数”;
上的一个“分界函数”;
(2)若 和
和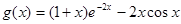 在
在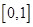 上一定存在一个“分界函数”,试确定实数
上一定存在一个“分界函数”,试确定实数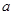 的取值范围.
的取值范围.
己知函数
(1)若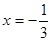 是
是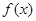 的极值点,求
的极值点,求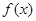 在
在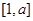 上的最大值;
上的最大值;
(2)在(1)的条件下,是否存在实数b,使得函数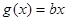 的图象与函数
的图象与函数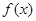 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
如图所示,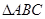 和
和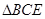 是边长为2的正三角形,且平面
是边长为2的正三角形,且平面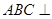 平面
平面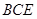 ,
,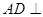 平面
平面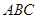 ,
,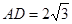 .
.
(1)证明: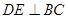 ;
;
(2)求三棱锥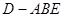 的体积.
的体积.
设函数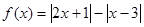
(1)求函数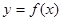 的最小值;
的最小值;
(2)若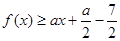 恒成立,求实数
恒成立,求实数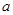 的取值范围.
的取值范围.
已知数列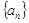 满足
满足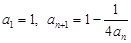 ,其中
,其中
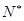 .
.
(1)设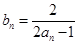 ,求证:数列
,求证:数列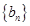 是等差数列,并求出
是等差数列,并求出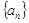 的通项公式
的通项公式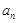 ;
;
(2)设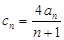 ,数列
,数列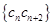 的前
的前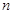 项和为
项和为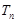 ,是否存在正整数
,是否存在正整数 ,使得
,使得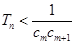 对于
对于 N*恒成立,若存在,求出
N*恒成立,若存在,求出 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.