如果数列 满足:
满足: 且
且 ,则称数列
,则称数列 为
为 阶“归化数列”.
阶“归化数列”.
(1)若某4阶“归化数列” 是等比数列,写出该数列的各项;
是等比数列,写出该数列的各项;
(2)若某11阶“归化数列” 是等差数列,求该数列的通项公式;
是等差数列,求该数列的通项公式;
(3)若 为n阶“归化数列”,求证:
为n阶“归化数列”,求证: .
.
在△ABC中,已知B=45°,D是BC边上的一点,AB=5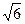 ,AC="14," DC=6,求AD的长.
,AC="14," DC=6,求AD的长.
(本小题满分14分)设函数 ,
,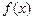 的两个极值点为
的两个极值点为 ,线段
,线段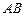 的中点为
的中点为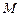 .
.
(1) 如果函数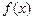 为奇函数,求实数
为奇函数,求实数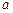 的值;当
的值;当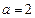 时,求函数
时,求函数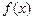 图象的对称中心;
图象的对称中心;
(2) 如果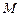 点在第四象限,求实数
点在第四象限,求实数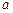 的范围;
的范围;
(3) 证明:点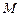 也在函数
也在函数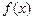 的图象上,且
的图象上,且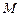 为函数
为函数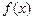 图象的对称中心.
图象的对称中心.
(本小题满分14分)
如图,设抛物线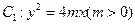 的准线与
的准线与 轴交于
轴交于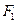 ,焦点为
,焦点为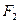 ;以
;以 为焦点,离心率
为焦点,离心率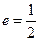 的椭圆
的椭圆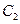 与抛物线
与抛物线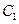 在
在 轴上方的交点为
轴上方的交点为 ,延长
,延长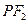 交抛物线于点
交抛物线于点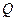 ,
,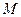 是抛物线
是抛物线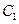 上一动点,且M在
上一动点,且M在 与
与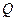 之间运动.
之间运动.
(1)当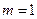 时,求椭圆
时,求椭圆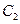 的方程,
的方程,
(2)当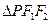 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,
求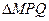 面积的最大值.
面积的最大值.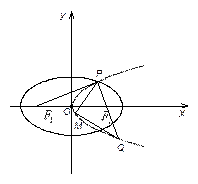
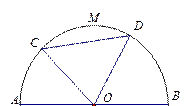
(本小题满分13分)某园林公司计划在一块 为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形
为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形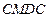 区域用于观赏样板地,
区域用于观赏样板地,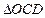 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
(1) 设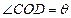 ,
,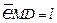 ,分别用
,分别用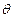 ,
,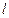 表示弓形
表示弓形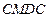 的面积
的面积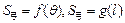 ;
;



|
 (2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式
(2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式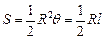 )
)
 |
(本小题满分1 3分)如图6,正方形
3分)如图6,正方形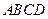 所在平面与圆
所在平面与圆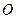 所在平面相交于
所在平面相交于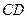 ,
,
线段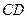 为圆
为圆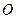 的弦,
的弦,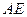 垂直于圆
垂直于圆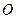 所在平面,
所在平面,
垂足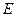 是圆
是圆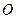 上异于
上异于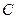 、
、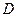 的点,
的点,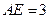 ,圆
,圆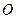 的直径为9.
的直径为9.
(1)求证:平面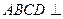 平面
平面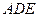 ;
;
(2)求二面角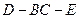 的平面角的正切值.
的平面角的正切值.