在四棱锥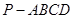 中,
中,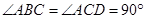 ,
,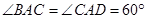 ,
,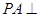 面
面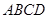 ,
,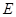 为
为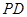 的中点,
的中点, .
.
(1)求证: ;
;
(2)求证: 面
面 ;
;
(3)求三棱锥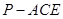 的体积
的体积 .
.
△ABC是正三角形,线段EA和DC都垂直于平面ABC.设EA=AB=2a,DC=a,且F为BE的中点,如图. 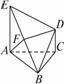
(1)求证:DF∥平面ABC;
(2)求证:AF⊥BD;
(3)求平面BDF与平面ABC所成二面角的大小.
△ABC是正三角形,线段EA和DC都垂直于平面ABC.设EA=AB=2a,DC=a,且F为BE的中点,如图. 
(1)求证:DF∥平面ABC;
(2)求证:AF⊥BD;
(3)求平面BDF与平面ABC所成二面角的大小.
已知正方体ABCD-A1B1C1D1.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E、F分别是AA1、CC1的中点,求证:平面EB1D1∥平面FBD.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 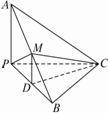
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积.
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a. 
(1)求证:平面SAB⊥平面SAD;
(2)设SB的中点为M,当 为何值时,能使DM⊥MC?请给出证明.
为何值时,能使DM⊥MC?请给出证明.