如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.
(1)求证:MN∥平面AA1C1C;
(2)若CC1=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB^平面CMN.

(本小题满分14分)
如图8,在直角梯形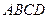 中,
中, ,
, ,且
,且 .现以
.现以 为一边向形外作正方形
为一边向形外作正方形 ,然后沿边
,然后沿边 将正方形
将正方形 翻折,使平面
翻折,使平面 与平面
与平面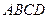 互相垂直,如图9.
互相垂直,如图9.
(1)求证:平面 平面
平面 ;
;
(2)求平面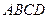 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.
(本小题满分12分)
为了评估天气对大运会的影响,制定相应预案,深圳市气象局通过对最近50多年的气象数据资料的统计分析,发现8月份是我市雷电天气高峰期,在31天中平均发生雷电14.57天(如图7).如果用频率作为概率的估计值,并假定每一天发生雷电的概率均相等,且相互独立.
(1)求在大运会开幕(8月12日)后的前3天比赛中,恰好有2天发生雷电天气的概率(精确到0.01);
(2)设大运会期间(8月12日至23日,共12天),发生雷电天气的天数为 ,求
,求 的数学期望和方差.
的数学期望和方差.
(本小题满分12分)
设函数 ,
,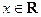 .
.
(1)若 ,求
,求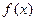 的最大值及相应的
的最大值及相应的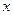 的集合;
的集合;
(2)若 是
是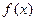 的一个零点,且
的一个零点,且 ,求
,求 的值和
的值和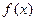 的最小正周期.
的最小正周期.
已知抛物线 :
: (
( ),焦点为
),焦点为 ,直线
,直线 交抛物线
交抛物线 于
于 、
、 两
两
点, 是线段
是线段 的中点,过
的中点,过 作
作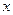 轴的垂线交抛物线
轴的垂线交抛物线 于点
于点 ,
,
(1)若抛物线 上有一点
上有一点 到焦点
到焦点 的距离为
的距离为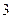 ,求此时
,求此时 的值;
的值;
(2)是否存在实数 ,使
,使 是以
是以 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
如图,函数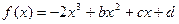 图像与x轴相切于原点。
图像与x轴相切于原点。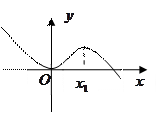
(1)求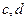 的值;
的值;
(2)若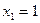 ,设
,设 ,若在
,若在 上至少存在一点
上至少存在一点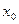 ,使得
,使得 成立,求实数
成立,求实数 的取
的取 值范围.
值范围.