如图，已知在平面直角坐标系xOy中，O是坐标原点，抛物线y=﹣x2+bx+c（c＞0）的顶点为D，与y轴的交点为C，过点C作CA∥x轴交抛物线于点A，在AC延长线上取点B，使BC=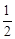
AC，连接OA，OB，BD和AD．
（1）若点A的坐标是（﹣4，4）
①求b，c的值；
②试判断四边形AOBD的形状，并说明理由；
（2）是否存在这样的点A，使得四边形AOBD是矩形？若存在，请直接写出一个符合条件的点A的坐标；若不存在，请说明理由．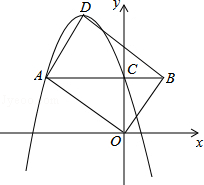
（本题6分）先化简，再求值：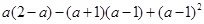
，其中
的绝对值等于1．
（每题4分，共8分）因式分解：
（1）
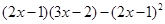
（2）
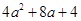
拖拉机在行驶的过程中的噪音会影响周围环境，某拖拉机位于A学校正南方向130m的B处，正以120m/min的速度沿公路BC方向行驶，如图所示，已知A学校到BC的距离AD=50m，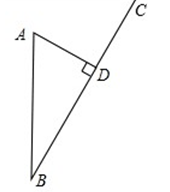
（1）求拖拉机从B处行驶到D处经过多长时间？
（2）如果在距拖拉机100m的圆形区域内都将受噪音影响，那么A学校受到拖拉机噪音影响的时间有多长？（结果精确到0.1，
≈1.732）
已知一次函数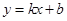
图象经过点（3，5）和点（0，-1）.
（1）求此一次函数的表达式；
（2）若点（a，2）在函数图象上，求a的值；
（3）判断点C（-1，-1）是否在这个函数的图象上；
一架云梯长25 m，如图所示斜靠在一面墙上，梯子底端C离墙7 m.
（1）这个梯子的顶端A距地面有多高？
（2）如果梯子的顶端下滑了4 m，那么梯子的底部在水平方向也是滑动了4 m吗？