如图①,在平面直角坐标中,点A的坐标为(1,﹣2),点B的坐标为(3,﹣1),二次函数y=﹣x2的图象为l1.
(1)平移抛物线l1,使平移后的抛物线经过点A,但不过点B.
①满足此条件的函数解析式有 个.
②写出向下平移且经点A的解析式 .
(2)平移抛物线l1,使平移后的抛物线经过A,B两点,所得的抛物线l2,如图②,求抛物线l2的函数解析式及顶点C的坐标,并求△ABC的面积.
(3)在y轴上是否存在点P,使S△ABC=S△ABP?若存在,求出点P的坐标;若不存在,请说明理由.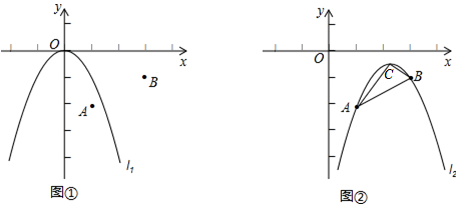
解方程:
解方程组
(本题12分)如图,直角坐标系中,以点A(1,0)为圆心画圆,点M(4,4)在⊙A上,直线y=-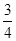 x+b过点M,分别交x轴、
x+b过点M,分别交x轴、
 y轴于B、C两点.
y轴于B、C两点.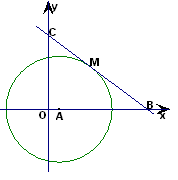
⑴求⊙A的半径和b的值;
⑵判断直线BC与⊙A的位置关系,并说明理由;
⑶若点P在⊙A上,点Q是y轴上C点下方的一点,当△PQM为等腰直角三角形时,请直接
写出满足条件的点Q坐标.
(本题12分)如图①,平面直角坐标系中,已 知C(0,10),
知C(0,10), 点P、Q同时从点出发,在线段OC上做往返匀速运动,设运动时间为t(s),点P、Q离开点O的距离为S图②中线段OA、OB(A、B都在格点上)分别表示当0≤t≤6时P、Q两点离开点O的距离S与运动时间t
点P、Q同时从点出发,在线段OC上做往返匀速运动,设运动时间为t(s),点P、Q离开点O的距离为S图②中线段OA、OB(A、B都在格点上)分别表示当0≤t≤6时P、Q两点离开点O的距离S与运动时间t (s)的函数图像.
(s)的函数图像.
⑴请在图②中分别画出当6≤t≤10时P、Q两点离开点O的距离S与运动时间t(s)的函数图像.
⑵求出P、Q两点第一次相遇的时刻.

 ⑶如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积 为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围).
⑶如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积 为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围).
(本题10分)某个体经营户销售同一型号的A、B两种品牌的服装,平均每月共销售60件,已知两种品牌的成本和利润如表所示,设平均每月的利润为y元,每月销售A品牌x件.
⑴写出y关于x的函数关系式
 .
.⑵如果每月投入的成本不超过6
 500元,所获利润不少于2920元,不考虑其他因素,那么销售方案有哪几种?
500元,所获利润不少于2920元,不考虑其他因素,那么销售方案有哪几种?⑶要使平均每月利润
 率最大,请直接写出A、B两种品牌的服装各销售多少件?
率最大,请直接写出A、B两种品牌的服装各销售多少件?