小明在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
| 分组 |
频数 |
百分比 |
600≤ <800 <800 |
2 |
5% |
800≤ <1000 <1000 |
6 |
15% |
1000≤ <1200 <1200 |
|
45% |
| |
9 |
22.5% |
| |
|
|
1600≤ <1800 <1800 |
2 |
|
| 合计 |
40 |
100% |
(2)补全频数分布直方图.
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
已知:四边形ABCD中,AC⊥BC,AB=17,BC=8,CD=12,DA=9;
(1)求AC的长
(2)求四边形ABCD的面积
如图,△ABC的顶点坐标分别是A(2,2)、B(3,5)、C(6,1)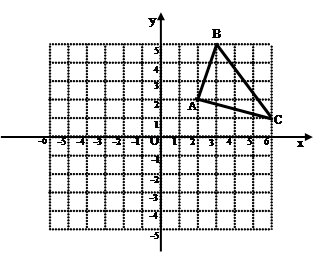
(1)作△A′B′C′,使△ABC与△A′B′C′关于x轴对称;
(2)AB长度是(填“有理数”或“无理数”),BC=;
(3)△ABC直角三角形(填“是”或“不是”);
(4)△ABC的面积=。
解方程组:(1)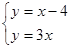
(2)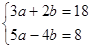
阅读理解:
如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题: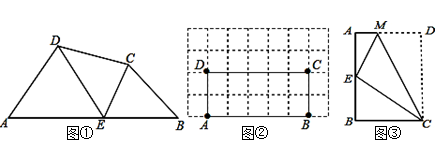
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试确定E点位置.
水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.
(1)水果商要把水蜜桃售价至少定为多少才不会亏本?
(2)在销售过程中,根据市场调查与预测,水果商发现每天水蜜桃的销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示,那么当销售单价定为多少时,每天获得的利润是640元?