水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.
(1)水果商要把水蜜桃售价至少定为多少才不会亏本?
(2)在销售过程中,根据市场调查与预测,水果商发现每天水蜜桃的销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示,那么当销售单价定为多少时,每天获得的利润是640元?
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,
连接CD,已知∠CDB=∠OBD=30°.
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.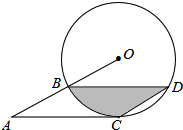
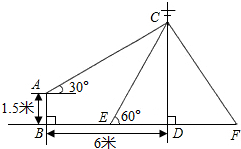
如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据: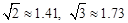 ).
).
某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?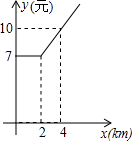
甲口袋中装有3个相同的小球,它们分别写有数值﹣1,1,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y),请用树形图或列表法,求点A落在第一象限的概率.
某校为了解学生对三种国庆活动方案的意见,对该校学生进行了一次抽样调查(被调查学生至多赞成其中的一种方案),现将调查结果绘制成如图两幅不完整的统计图.
请根据图中提供的信息解答下列问题
(1)在这次调查中共调查了名学生;扇形统计图中方案1所对应的圆心角的度数为度;
(2)请把条形统计图补充完整;
(3)已知该校有1000名学生,试估计该校赞成方案1的学生约有多少人?