某中学高三年级从甲(文)、乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.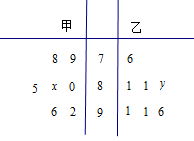
(1)求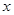 和
和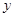 的值;
的值;
(2)计算甲组7位学生成绩的方差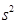 ;
;
(3)从成绩在90分以上的学生中随机抽取两名学生,求甲组至少有一名学生的概率.
男运动员6名,女运动员4名,其中男女队长名1人,选派5人外出比赛,在下列情形中各有多少种选派方法?
(1)男运动员3名,女运动员2名
(2)至少有一名女运动员
(3)队长中至少有1人参加
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费
为 元(
元( 为常数,且
为常数,且 ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为 元(
元( ),根据
),根据
市场调查,销售量 与
与 成反比,当每
成反比,当每 公斤蘑菇的出厂价为30元时,日销售量为100公斤.
公斤蘑菇的出厂价为30元时,日销售量为100公斤.
(1)求该工厂的每日利润 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价 元的函数关系式;
元的函数关系式;
(2)若 ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价 为多少元时,该工厂的利润
为多少元时,该工厂的利润
 最大,并求最大值
最大,并求最大值
已知函数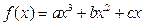 在点
在点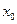 处取得极大值
处取得极大值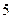 ,
,
其导函数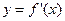 的图象经过点
的图象经过点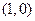 ,
,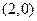 ,如图所示.
,如图所示.
求: (1)
(1)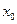 的值;(2)
的值;(2)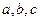 的值.
的值.
(3)、若曲线

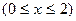 与
与 有两个不同的交点,
有两个不同的交点,
求实数 的取值范围。
的取值范围。
(已知函数 图像上的点
图像上的点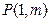 处的切线方程为
处的切线方程为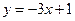 .[来
.[来
(1)若 函数
函数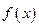 在
在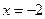 时有极
时有极 值,求
值,求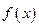 的表达式;
的表达式;
(2)函数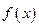 在区
在区 间
间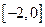 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。
计算下列定积分。
(1) (2)
(2) 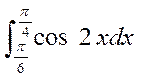 (3)
(3)