已知圆C1的参数方程为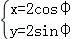（φw为参数），以坐标原点O为极点，x-优题课

已知圆C₁的参数方程为（φw为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C₂的极坐标方程为ρ=4sin（θ+）．
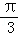（1）将圆C₁的参数方程化为普通方程，将圆C₂的极坐标方程化为直角坐标系方程；
（2）圆C₁，C₂是否相交？请说明理由．

科目数学题型解答题难度较难

知识点：参数方程

根据以往统计资料，某地车主购买甲种保险的概率为0.5，购买乙种保险但不购买甲种保险的概率为0.3，设各车主购买保险相互独立。
（Ⅰ）求该地1为车主至少购买甲、乙两种保险中的1种的概率；
（Ⅱ） $X$ 表示该地的100为车主中，甲、乙两种保险都不购买的车主数，求 $X$ 的期望。

$△ A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$ .已知 $A - C = 90^{°}, a + c = \sqrt{2} b$ ，求 $C$

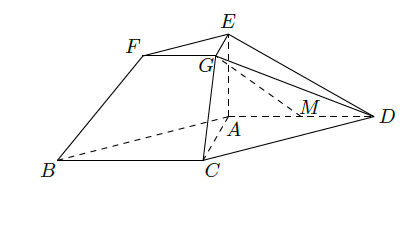
在如图所示的几何体中,四边形 $A B C D$ 为平行四边形, $∠ A C B = 90^{°}$ , $E A ⊥$ 平面 $A B C D$ , $E F ∥ A B, F G ∥ B C, E G ∥ A C, A B = 2 E F$ .

（Ⅰ)若 $M$ 是线段 $A D$ 的中点,求证: $G M ∥$ 平面 $A B F E$ ;
（Ⅱ）若 $A C = B C = 2 A E$ ,求二面角 $A - B F - C$ 的大小．

在 $△ A B C$ 中,内角 $A, B, C$ 的对边分别为 $a, b, c$ ,已知( $\frac{\cos A - 2 \cos C}{\cos B} = \frac{2 c - a}{b}$ ）

（1）求 $\frac{\sin C}{s i n A}$ 的值

(2) 若 $\cos B = \frac{1}{4}$ , $b = 2$ ,求 $△ A B C$ 的面积.

已知函数 $f (x) = \frac{2}{3} x + \frac{1}{2}, h (x) = \sqrt{x}$ ．

(I)设函数 $F (x) = f (x) - h (x)$ ，求 $F (x)$ 的单调区间与极值；
(Ⅱ)设 $a \in R$ ，解关于 $x$ 的方程 $\log_{4} [\frac{3}{2} f (x - 1) - \frac{3}{4}] = \log_{2} h (a - x) - \log_{2} h (4 - x)$ ；

(Ⅲ)试比较 $f (100) h (100) - \sum_{k = 1}^{100} h (k)$ 与 $\frac{1}{6}$ 的大小.

试卷网试题网古诗词网作文网范文网