已知函数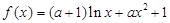 .
.
(1)讨论函数 的单调性;
的单调性;
(2)设 ,证明:对任意
,证明:对任意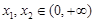 ,
, .
.
(本小题共10分)
在直角坐标系中直线L过原点O,倾斜角为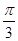 ,在极坐标系中(与直角坐标系有相同的长度单位,极点为原点,极轴与x的非负半轴重合)曲线C:
,在极坐标系中(与直角坐标系有相同的长度单位,极点为原点,极轴与x的非负半轴重合)曲线C: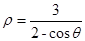 ,
,
(1)求曲线C的直角坐标方程;
(2)直线L与曲线C交于点 ,求
,求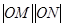 的值。
的值。
(本小题共12分)
已知函数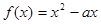 ,
,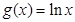
(1)若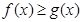 对于定义域内的
对于定义域内的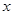 恒成立,求实数
恒成立,求实数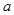 的取值范围;
的取值范围;
(2)设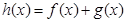 有两个极值点
有两个极值点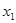 ,
,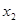 且
且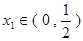 ,求证:
,求证: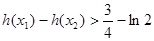 ;
;
(3)设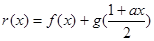 若对任意的
若对任意的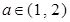 ,总存在
,总存在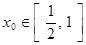 ,使不等式
,使不等式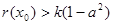 成立,求实数
成立,求实数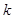 的取值范围.
的取值范围.
(本小题共12分)
如图,已知直线l与抛物线 相切于点P(2,1),且与x轴交于点A,O为坐标原点,
相切于点P(2,1),且与x轴交于点A,O为坐标原点,
定点B的坐标为(2,0).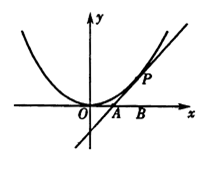
(1)若动点M满足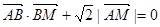 ,求点M的轨迹C;
,求点M的轨迹C;
(2)若过点B的直线l′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
(本小题共12分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD= .
.
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
(本小题共12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
| 月收入(单位百元) |
[15,25 |
[25,35 |
[35,45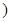 |
[45,55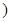 |
[55,65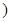 |
[65,75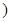 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(1)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
| 月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
|
| 赞成 |
 |
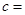 |
|
| 不赞成 |
 |
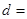 |
|
| 合计 |
(2)若对在[15,25) ,[25,35)的被调查中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为 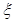 ,求随机变量
,求随机变量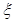 的分布列。
的分布列。
附:
