已知 p ：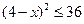
； q ：
。
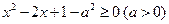若
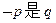的充分不必要条件，求实数 
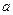的取值范围。
已知椭圆焦点是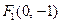 
和 
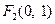，离必率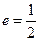 
（1）求椭圆的标准方程；
（2）又设点P在这个椭圆上，且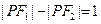
，求 
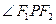的余弦值。
对于定义域为
的函数
，若有常数M，使得对任意的
，存在唯一的
满足等式
，则称M为函数
f (x)的“均值”．
（1）判断1是否为函数
≤
≤
的“均值”，请说明理由；
（2）若函数
为常数）存在“均值”，求实数a的取值范围；
（3）若函数
是单调函数，且其值域为区间I．试探究函数的“均值”情况（是否存在、个数、大小等）与区间I之间的关系，写出你的结论（不必证明）．
说明：对于（3），将根据结论的完整性与一般性程度给予不同的评分
已知数列
是各项均为正数的等差数列，公差为d（d 
0）．在
之间和b,c之间共插入
个实数，使得这
个数构成等比数列，其公比为q．
（1）求证：
；
（2）若
，求
的值；
（3）若插入的n个数中，有s个位于a,b之间，t个位于b,c之间，且
都为奇数，试比较s与t的大小，并求插入的n个数的乘积（用
表示）.
已知椭圆
：
(
)过点
，其左、右焦点分别为
，且
．
（1）求椭圆的方程；
（2）若
是直线
上的两个动点，且
，则以
为直径的圆
是否过定点？请说明理由．
.
的最小正周期；
上的最大值与最小值.