中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”，按照成绩大于等于125分为“优秀”，成绩小于125分为“非优秀”, 根据调查这两个班的数学成绩得到的数据，所绘制的二维条形图如图.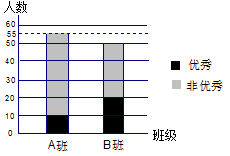
（1）根据图中数据，制作2×2列联表；
（2）计算随机变量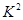
的值（精确到0.001）
（3）判断在多大程度上可以认为“成绩与班级有关系”？ （温馨提示：答题前请仔细阅读卷首所给的计算公式及其参考值）
集合P=｛x︱x2-2x-3=0｝，S=｛x︱ax+2=0｝，SÍP，求a的值。
如图，有一壁画，最高点A处离地面4m，最低点B处离地面2m，若从离地高1.5m的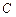
处观赏它，则离墙多远时，视角
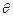最大？
选做题（本小题满分10分。请考生三两题中任选一题做答，如果多做，
则按所做的第一题记分）
选修4－1：几何证明选讲
如图，圆O的直径AB=10，弦DE⊥AB于点H，BH=2。1）求DE的长；
（2）延长ED到P，过P作圆O的切线，
切点为C，若ＰＣ＝２
，求ＰＤ的长。
选修4－5：不等式选讲
（Ⅰ）若
与2的大小,不用说明理由;
（Ⅱ）设m是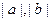
和1中最大的一个,当
已知函数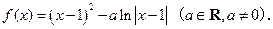
（1）当
时，求函数
的单调区间；
（2）求函数在区间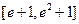
上的最小值．
已知两点M(－2,0)，N(2,0)，点P为坐标平面内的动点，且满足||||＋·＝0.
(1)求点P的轨迹C的方程；
(2)设过点N的直线l的斜率为k，且与曲线C相交于点S、T，若S、T两点只在第二象限内运动，线段ST的垂直平分线交x轴于Q点，求Q点横坐标的取值范围．