提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度
（单位：千米/小时）是车流密度
（单位：辆/千米）的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时，研究表明；当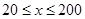
时，车流速度是车流密度的一次函数．
（1）当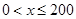
时，求函数
的表达式．
（2）当车流密度为多大时，车流量（单位时间内通过桥上某观查点的车辆数，单位：
辆/每小时）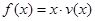
可以达到最大，并求最大值（精确到1辆/每小时）．
如图所示，正方形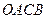
内的阴影区域的上边界是曲线
，现向正方形区域内随机等可能地投点，则点落在阴影区域的概率是（***）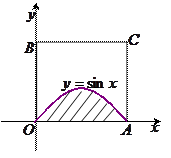
A． |
B． |
C． |
D． |
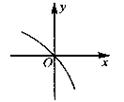
已知函数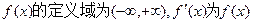
的导函数，函数
的图象如图所示，且
，则不等式
的
解集为（**
*）
A． |
B． |
C． |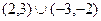
D． |
（本小题15分）
设数列{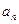
}的前n项和为
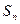，并且满足
，
（n∈N*）.
（Ⅰ）求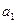
，
，
；
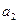（Ⅱ）猜想{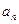}的通项公式，并用数学归纳法加以证明；
（Ⅲ）设
，
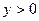，且
，证明：
≤
.
（本小题10分）
已知函数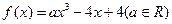
在
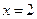
取得极值。
（Ⅰ）确定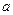
的值并求函数的单调区间;
（Ⅱ）若关于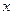
的方程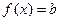
至多有两个零点，求实数
的取值范围。
（本小题满分12分）
已知圆C的圆心为原点O，且与直线x+y+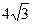
=0相切.
（1）求圆C的方程；
（2）点P在直线x=8上，过P点引圆C的两条切线PA、PB，切点为A、B,求证：直线AB恒过定点.