如图,在四棱锥P-ABCD中,PA⊥底面ABCD,PC⊥AD,底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC.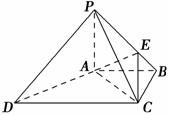
本小题满分12分)
已知关于x的二次函数f(x)=ax2-4bx+1.
(I)已知集合P={-1,1,2,3,4,5},Q={-2,-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率;
(II)在区域内随机任取一点(a,b).求函数 y=f(x)在区间[1,+∞)上是增函数的概率.
y=f(x)在区间[1,+∞)上是增函数的概率.
(本小题 满分10分)
满分10分)
已知向量
 ,定义
,定义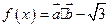
(I)求函数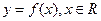 的单调递减区间;
的单调递减区间;
(II)若函数 为偶函数,求
为偶函数,求 的值。
的值。
(本小题满分10分)
在某学校组织的一次蓝球定点投蓝训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投三次。某同学在 A处的命中率
A处的命中率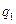 为0.25,在B处的命中率为
为0.25,在B处的命中率为 .该同学选择
.该同学选择 先在A处投一球,以后都在B处投,用
先在A处投一球,以后都在B处投,用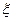 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为 
 |
0 |
2 |
3 |
4 |
5 |
 |
0.03 |
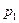 |
 |
 |
 |
 求
求 的值;
的值; 求随机变量
求随机变量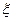 的数学期量
的数学期量 ;
; 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超
试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超 过3分的概率的大小。
过3分的概率的大小。
(本小题满分10分)
如图,在底面边长 为1,侧棱长为2的正四棱柱
为1,侧棱长为2的正四棱柱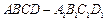 中,P是侧棱
中,P是侧棱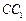 上的一点,
上的一点,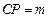 . (1)试确定m,使直线AP与平面BDD1B1所成角为60º;(2)在线段
. (1)试确定m,使直线AP与平面BDD1B1所成角为60º;(2)在线段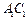 上是否存在一个定点
上是否存在一个定点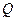 ,使得对任意的m,
,使得对任意的m,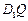 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论.
(本小题满分10分)
过点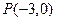 且倾斜角为
且倾斜角为 的直线和曲线
的直线和曲线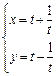 (
(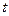 为参数)相交于
为参数)相交于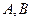 两点.求线段
两点.求线段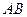 的长.
的长.